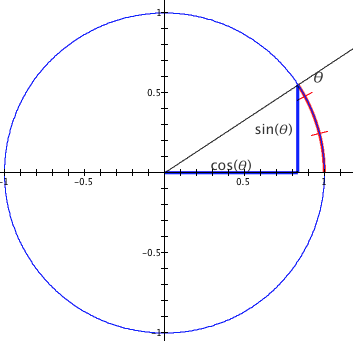
Figure 2.6.1. Slope of the ray from $(0,0)$ that subtends an arc of $\theta$ radii is $\dfrac{\sin(\theta)}{\cos(\theta)}$.
| < Previous Section | Home | Next Section > |
It is unfortunate that the word "tangent" in trigonometry has a different meaning than in geometry. In geometry, and speaking loosely, a tangent is a line that touches a curve in just one point. The tangent function in trigonometry is a function that gives the slope of a line.
Figure 2.6.1 shows that the slope of a line that passes through the origin and makes an angle of θ radians is $\dfrac{\sin(\theta)}{\cos(\theta)}$. This is why, in trigonometry, tan(θ) is defined as $$\tan(θ)=\dfrac{\sin(\theta)}{\cos(\theta)},$$where θ is the measure in radians of the arc that the line subtends, measured from 0 radians. It gives the slope of a line.

The quotient $\left( \frac{\sin(\theta)}{\cos(\theta)} \right)$ gives the measure of $\sin(\theta)$ in units of $\cos(\theta)$. A value of the quotient does not have the radius as a unit of measure, as does sine and cosine.
To graph $y = \tan(x)$ in the same coordinate system as sine and cosine, the quotient must have the circle’s radius as a unit of measure. We can do that by using similar triangles.
The animation in Figure 2.6.2 uses the relationship $$\dfrac{\sin(\theta)}{\cos(\theta)}=\dfrac{\tan(\theta)}{1}.$$ By displaying the value of $\tan(\theta)$ in the x-y coordinate system at $x =1$, the directed segment that represents the value of $\tan(\theta)$ is measured in units of the circle’s radius.
We can thus graph $y = \tan(x)$ in the same coordinate system as cosine and sine because "1" means the same thing for all of them — the length of the circle’s radius.
Reflection 2.6.1. Convince yourself that the value labeled $\tan(\theta)$ gives the slope of the line, and that this value is measured in units of the circle’s radius.
What happens to the quotient sin($\theta$)/cos($\theta$) as $\cos(\theta)$ is near 0 but greater than 0?
Reflection 2.6.3. Why does $\tan(\theta)$ make sudden jumps from positive infinity to negative infinity?
Reflection 2.6.4. Is $\tan(\theta)$ always increasing over every interval contained in the domain of its independent variable? That is, does it ever decrease as $\theta$ increases continuously?
In what circumstances is it appropriate to write "$\sin(x)$", "$\cos(x)$", and "$\tan(x)$"?
| < Previous Section | Home | Next Section > |