
Figure 3.12.1. Components of a function defined computationally using function notation
| < Previous Section | Home | Next Section > |
The example of distance from Earth to Moon illustrated that function notation gives us representational power. With function notation, we can represent relationships between specific values of quantities conceptually before we even know how specific values might actually be related.
You will see later that using function notation also allows us to investigate types of functions and their properties.
Functions can be defined two ways: conceptually or computationally.
A function defined conceptually describes the nature of the relationship between two variables. The example of distance between Earth and Moon, given earlier, defined this distance conceptually in relation to the passage of time.
A function defined computationally specifics how to calculate values of the dependent variable from values of the independent variable. Computational definitions of functions are the centerpiece of mathematical modeling. Functions defined computationally allow us to gain precise numerical information about the phenomena we model. At the same time, when modeling any situation, a conceptual definition should precede a computational definition.
It is imperative that you specify the domain of a function’s independent variable, regardless of whether you define the function conceptually, computationally, or both. In this textbook, we will assume that the real numbers comprise any independent variable’s domain unless stated otherwise or unless restrictions are required by context.
You have seen many examples of functions defined computationally. The statement $y = u(13.76 ‑ 2u)(16.42 ‑ 2u)$, u a real number, defines y as a function of u computationally. However, this function has no name, so we have no way to speak of it aside from the repeating the entire statement. We also have no way to represent the value of y that corresponds to a specific value of u. Function notation solves these problems. We would instead write$$V(u)=u(13.76-2u)(16.42-2u)$$
In this statement,
Figure 3.12.1 summarizes all this graphically.

We refer to a function by stating its name. Thus, V is the function defined in Figure 3.12.1. It is a mistake to say that $V(u)$ is the function defined in Figure 3.12.1; $V(u)$ represents the value of the dependent variable that corresponds to a value of u. The function is V, not $V(u)$.
You should practice forming an image of how a function defined computationally (as in Figure 3.12.1 above) is related to the conceptual definition of functions given in Section 3.11. The animation below might help.
Prior sections stressed the importance that you understand and utilize the representation power of function notation. It is equally important to have an image of how function notation turns values of an independent variable into values of a dependent variable. Figure 3.12.2 starts with a definition of a function g in terms of an independent variable u. According to the convention shown in Figure 3.12.1, the definition in Figure 3.12.2 names the function (g), names the independent variable (u), and states what to do with a value of u to produce the value of the dependent variable that is associated with that value of u, represented by $g(u)$.
Many students object to the expression $g(3x)$ in Figure 3.12.2a because the definition of g uses the letter u, not the letter x. However, it is important to understand that the letter u in Figure 3.12.2a represents a value of the independent variable. The animation in Figure 3.12.2a shows that there is no conflict between using x in one expression and u in the definition of g.
Once we assign a value to x, the statement $g(3x)$ invokes the definition of g and passes the value of 3x to it. When the number 2 is assigned as a value of x, 3x is 6, and the statement $g(3x)$ invokes the definition of g with the number 6 as the value of u.
The animation in Figure 3.12.2b shows a more formal way of thinking about $g(3x)$. It invokes the definition of g with the expression 3x as the value of u. If you substitute $x = 2$ after substituting 3x for u, you will get g(6), just as in Figure 3.12.2a.
Figure 3.12.3 displays the definition of the function u using an independent variable u. This might seem confusing, but it is not. The function’s name is u. Any letter can be used to represent values of its independent variable. The animation in Figure 3.12.3 shows how the different roles of function name and independent variable name removes any possibility of confusion.
Ron Avitzur, the creator of GC, faced a dilemma caused by GC’s flexibility in graphing equations and functions. A person can use letters like f and g as parameters and they can use them as function names. So someone could write an expression like $f(x+5)$ to mean the parameter f times the sum $(x + 5)$, or she could mean a function named f evaluated at the value of the expression $x + 5$.
Avitzur needed a way that people could signal to GC whether it should interpret a letter as a parameter or as a function name. He settled on the convention that instead of typing f and shift-9 to define a function using function notation, you will type f and ctrl-9.
Typing ctrl-9 causes GC to produce parentheses, but with the meaning that parentheses contain a letter or an expression that gives an input value to the function.
| f shift-9 x + 5 | ⟶ | f (x+5) | Parameter f times the value of x+5 |
| f ctrl-9 x + 5 | ⟶ | f(x+5) | Function f evaluated with the value of x+5 |
A visual cue to distinguish between function notation and parameter multiplication is that parentheses are closer to a function name than to a parameter name.

GC does not require ctrl-9 for built-in functions like sin or cos. In fact, you will confuse GC if you use ctrl-9 with a built-in function. Use
ctrl-9 only with functions that you define. Do not use ctrl-9 with
functions that are built into GC.
GC allows functions defined in terms of several independent variables. For example, the function S, below, converts a time given in hours, minutes, and seconds into a number of seconds.
$$S(h,m,s) = 3600h+60m+s$$
To convert 23:40:17 into a number of seconds, enter $S(23,40,17)$. GC will display 85217, which is the number of seconds in 23 hours, 40 minutes, and 17 seconds.
| Define this function | Type this | You should get |
|
| 1. | $f(w)=\sqrt{w}$ | $y=f(x)$ | 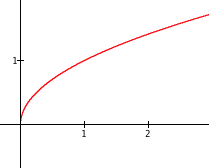 |
| 2. | $g(r)=2r-1$ | $y=g(f(x))$ | 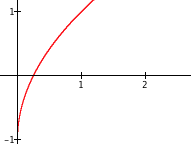 |
| 3. | $q(s)=g(s)-f(s)$ | $y=q(x)$ | 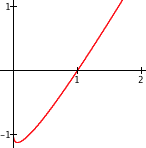 |
| 4. | $r(h)=0.1 \sin(100h) + e^{\cos h}$ | $y=r(x)$ | 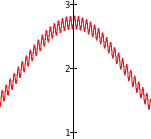 |
| 5. | $s(p)=r(q(g(p)))$ | $y=s(x)$ |  |
Alfredo and Juan are precalculus students. They have recently been introduced to the idea of function notation.
Alfredo feels more comfortable making calculations with numbers. Juan is enthralled with this new idea of function notation.
A textbook exercise defined the function f as $f(x)=0.5x^3-2x^2+x\cos(3x)+1$ and requested that students calculate the average rate of change of f as x varies from $x=1.75$ to $x=3.04$.
Juan's and Alfredo's work is shown below.

| < Previous Section | Home | Next Section > |