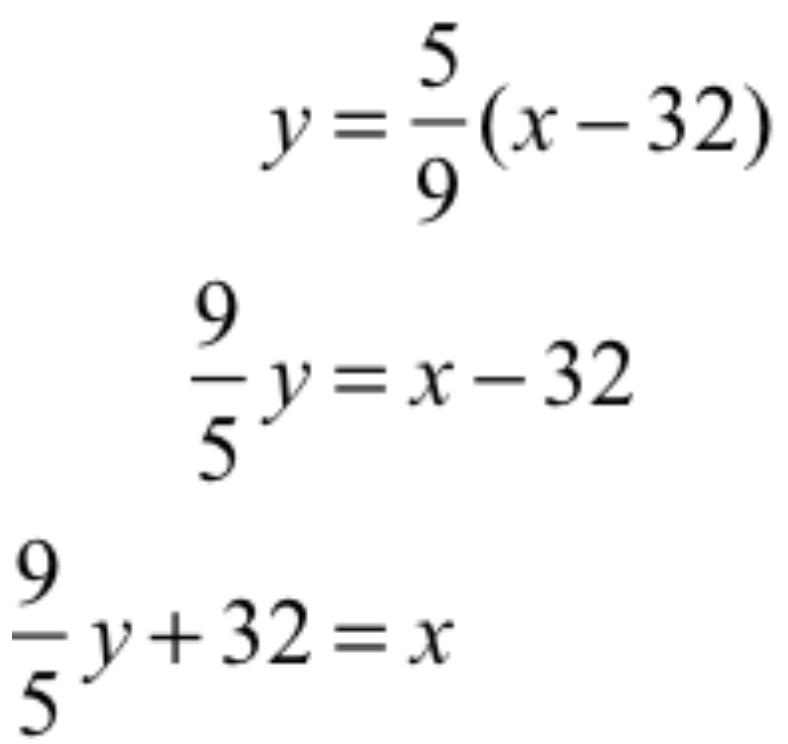
Figure 3.18.2. Start with an equation that gives y, a number in degrees C, in terms of x,a number in degrees F; end with an equation that gives x, a number in degrees F, in terms of y, a number in degrees C.
| < Previous Section | Home | Next Section > |
A graph of a relationship between two variables x and y actually shows two relationships. It shows values of y that are related to values of x, and it shows values of x that are related to values of y.
Figure 3.18.1 illustrates the two perspectives on what a graph shows us, and the difference between perspectives is in which variable you take as the independent variable and in the flexibility of seeing independent variables on either horizontal or vertical axes.
Figure 3.18.1 shows that even though we start with y as a function of x, and define the relationship with $$f(x)=3x+2,$$ we could just as easily look at the graph as showing x as a function of y, with the relationship defined as $$g(y)= \frac{y-2}{3}.$$
We also can see inverse relationships in non-graphical settings. The formula for converting a temperature in degrees Fahrenheit (F°) to a an equivalent temperature in degrees Celsius (C°) is $y = \frac{5}{9}(x‑32)$, where x is a temperature in F° and y is a temperature in C°.
Suppose you are in France, where all temperatures are in degrees Celsius! How do you go the other way, from C° to F°? You must solve for x in terms of y (Figure 3.18.2).
If we call the original function in Figure 3.18.2 f, then $$f(x) = \frac{5}{9}(x‑32).$$
If we call the end function in Figure 3.18.2 g, then
$$g(y) = \frac{9}{5}y + 32.$$
The function f converts x degrees Fahrenheit to y degrees Celsius. The function g converts y degrees Celsius to x degrees Fahrenheit.
Suppose we start with 82 degrees F, convert it into $y_0$ degrees C, and then convert $y_0$ degrees C back to $x_0$ degrees F? What should $x_0$ be? 82! Indeed, if we convert any temperature x degrees F to y degrees C, then convert y degrees C back to a number of degrees F, that number should be the value we started with. We can express this symbolically as $$g(f(x))= x.$$
The same will be true about converting from degrees C to degrees F and back to degrees C. After all the converting, we should end with the temperature in degrees C that we start with. We can express this symbolically as $$f(g(y))=y.$$
Reflection 3.18.1: Convince yourself that with f and g defined as above, $f(g(17))=17$ and that $g(f(85))=85$. Question: What is the unit for both instances of 17 in $f(g(17))=17$? What is the unit for both instances of 85 in $g(f(85))=85$?
Reflection 3.18.2: Let f and g be as in the Celsius $\leftrightarrow$ Fahrenheit example. In the statement $f(g(y)) = y$, what is the unit of y? In the statement $g(f(x)=x$, what is the unit of x?
Reflection 3.18.3: Let f and g be as in the Celsius $\leftrightarrow$ Fahrenheit example. Would it be a valid statement to say $f(g(u))=u$ or $g(f(v))=v$ for real numbers u and v? In other words, must we use x and y?
The idea of inverse functions is a generalization of the Celsius $\leftrightarrow$ Fahrenheit example.
Functions h and k are inverse functions when they satisfy two conditions:
When a function h has an inverse function, it is represented as $h^{-1}$ (read "h inverse"). The "-1" in $h^{-1}$ is not an exponent. Rather, it is the general symbol for undoing what something does.
If h and k are inverse functions, then $h=k^{-1}$ and $k = h^{-1}$ ("h equals k inverse and k equals h inverse"). The function $h^{-1}$ undoes what the function h does to values of its independent variable. The function $k^{-1}$ undoes what the function k does to its independent variable.
Suppose that j is a function with w as its independent variable and z as its dependent variable. The inverse of j, namely $j^{-1}$, would have z as its independent variable and w as its dependent variable.
If j relates two values of w to one value of z, then the inverse of j will not be a function. If, for example, $j(2)=7$ and $j(3)=7$, then $j^{-1}(7)$ could be 2 or it could be 3. This means that $j^{-1}$ could not be a function because $j^{-1}(7)$ does not have a unique value.
For $j^{-1}$ to be a function, the function $j$ must satisfy the criterion that it is one-to-one. The function j being one-to-one means that every value of $j$'s dependent variable is related to exactly one value of its independent variable.
For a function j to have an inverse function over an interval, it must be one-to-one over that interval.
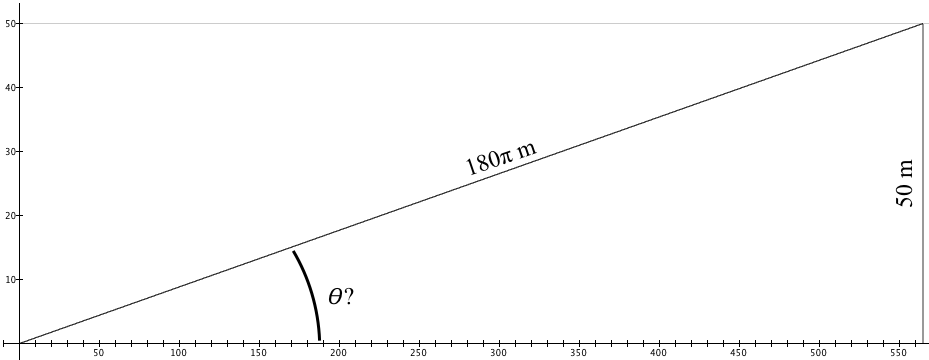
Problem: A construction company has contracted to design and build a highway on-ramp similar to the one in Figure 3.43. The on-ramp must carry cars from street level to highway level, a height of 50m, make a turn of $\frac{3π}{2}$ radians, or 270°, and have a radius of 120 m. They need to determine the angle of elevation (angle from parallel to ground) that the on-ramp must make at all points along it so that the end of the on-ramp meets the highway it will join.
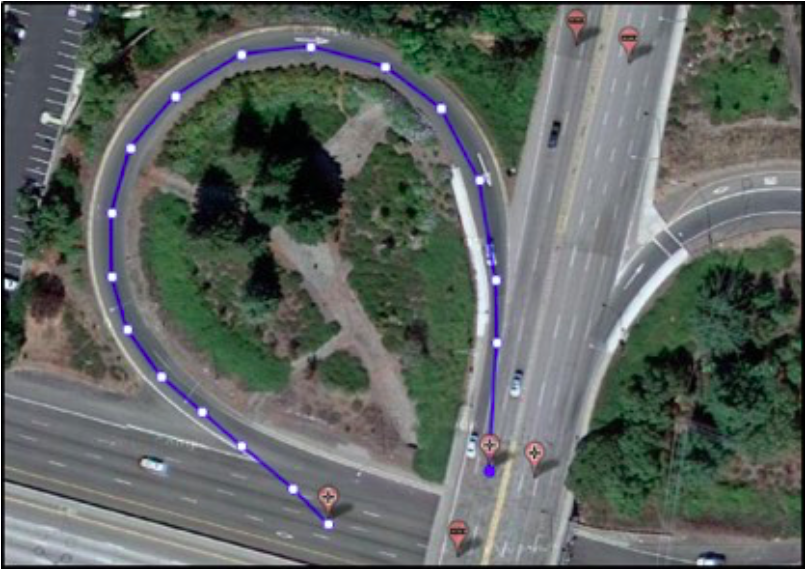
Solution and reasoning:
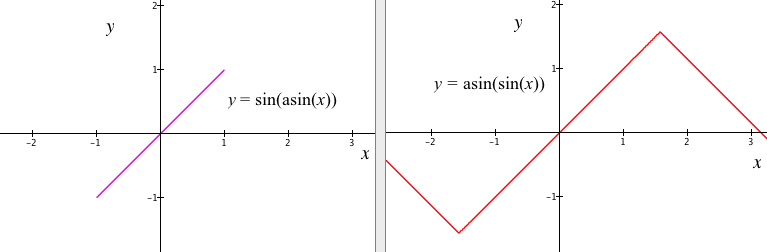
The matter of inverse functions of trigonometric functions is tricky, because trigonometric functions are not one-to-one over the domains of their independent variables (Figure 3.18.5).

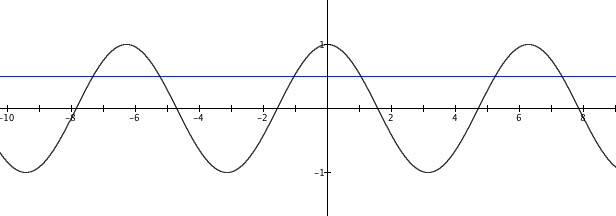
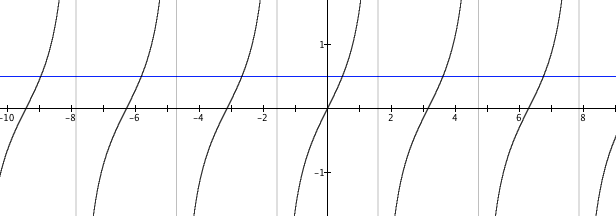
Each function in Figure 3.18.5 has an infinite number of values that produce a value of 0.5. It will therefore not be possible to define an inverse function for any of them. However, we can restrict the domain of each function to an interval over which it is one-to-one. For example, Figure 3.18.6 shows the domain of sine’s independent variable restricted to the interval $-\frac{π}{2}$ to $\frac{π}{2}$. Over this interval, sin(x) is one-to-one and therefore has an inverse function.
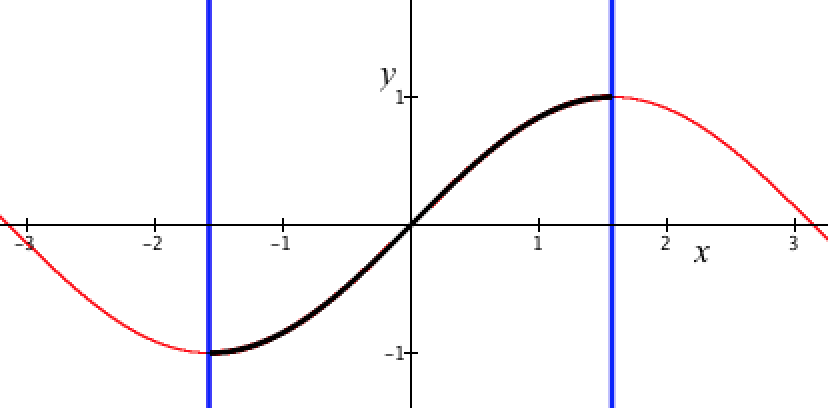
The function is one-to-one when independent variable restricted to $-\frac{π}{2} ≤ x≤\frac{π}{2}$. So sin(x) has an inverse over that interval.
The inverse of sin, called arc sine ("asin" in GC), is defined as $$\mathrm{asin}(y)=x\text{ such that }\sin(x)=y.$$ This might seem like a strange definition, but it is not. The graph in Figure 3.14.1 came from $y = \sin(x)$, so our computing devices have a method to compute sin(x).
We define asin conceptually, saying to reverse the process of assigning values to sin(x), whatever that process is.
You will learn methods for computing approximations to sin(x) and asin(y) in Calculus II. Your calculator and GC have these methods programmed into them.
For the meantime, celebrate the fact that your calculator has a magical button labeled $\sin^{-1}$ and that GC has a magical function named asin.
Reflection 3.18.4. Examine a displayed graph of $y = \cos(x)$ in GC. How could you restrict its independent variable to an interval so that cos is one-to-one over that interval? There is more than one way to do this; try to make it symmetric around 0 or as closely tied to 0 as possible.
Reflection 3.18.5. Examine a displayed graph of $y = \tan(x)$ in GC. How could you restrict its independent variable to an interval so that tan is one-to-one over that interval? There is more than one way to do this; try to make it symmetric around 0 or as closely tied to 0 as possible.
There will be occasions when you need to convert from rectangular coordinates to polar coordinates.
A point’s distance from the pole is easy. If the point P has rectangular coordinates (a, b), denoted hereafter as P:(a, b), then, by the Pythagorean Theorem, $r= \sqrt{a^2+b^2}$. Or, defined as a function, if a point has coordinates (x, y), then the point’s distance from the pole is $r(x,y)= \sqrt{x^2+y^2}$.
Determining a point's angle from the reference direction (the positive x-axis) is a bit trickier than determining its distance from the origin.
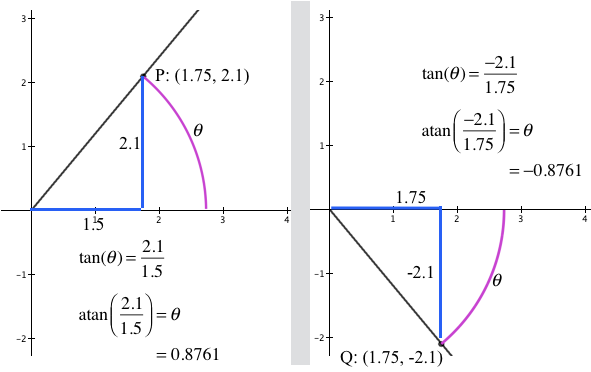
As illustrated in Figure 3.18.7 (a), if P:(a, b) is in the 1st or 4th quadrant, then the angle from the reference direction has a measure of $\atan(b/a)$.
However, there are two problems in determining a point's direction from the positive x-axis. The first problem arises when the point is is in the coordinate plane's 2nd or 3rd quadrant. The second problem arises when the point is on the y-axis.
Figure 3.18.7 (b) illustrates the first problem. It shows two points, $Q:(-1.75,-1.25)$ and $P:(1.75,1.25)$. The quotient of point Q’s coordinates is the same as the quotient of P’s coordinates, so the atan function cannot distinguish between points Q and P in terms of their direction from the positive x-axis.
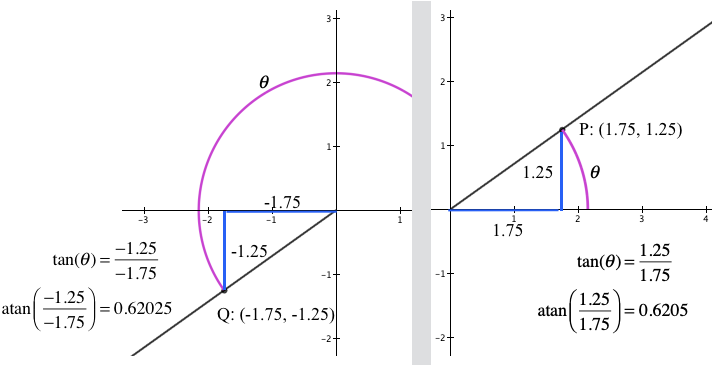
Figure 3.18.7 (c) shows a similar problem distinguishing between the direction of point $R:(-1.75,1.25)$ in the second quadrant from the direction of point $S:(1.75,-1.25)$ in the fourth quadrant. The quotient of S's coordinates is the same as the quotient of R’s coordinates.
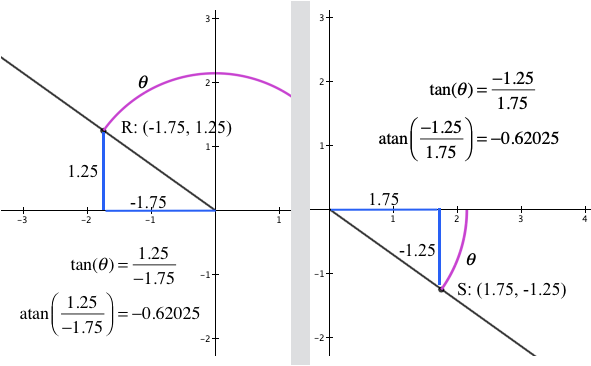
In short, atan cannot distinguish between directions of points $(a,b)$ and $(-a,-b)$, nor can atan distinguish between directions of points $(a,-b)$ and $(-a,b)$.
The second problem arises if a point is on the y-axis. The function $\atan(\theta)$ (arctangent $\theta$) is defined only for values of $\theta$ such that $-\dfrac{\pi}{2}\lt \theta \lt \dfrac{\pi}{2}$. It is not defined for $\theta= \dfrac{\pi}{2}$ (when a point is on the positive y-axis) or for $\theta= -\dfrac{\pi}{2}$ (when a point is on the negative y axis).
A solution to both problems is to define a new function that we call taninv (tangent inverse). It will have two independent variables: the point’s x-coordinate and the point's y coordinate.
Any value $\taninv(x,y)$ will be a point’s direction from the positive x-axis, given as an angle measure in radians between 0 and $2\pi$.
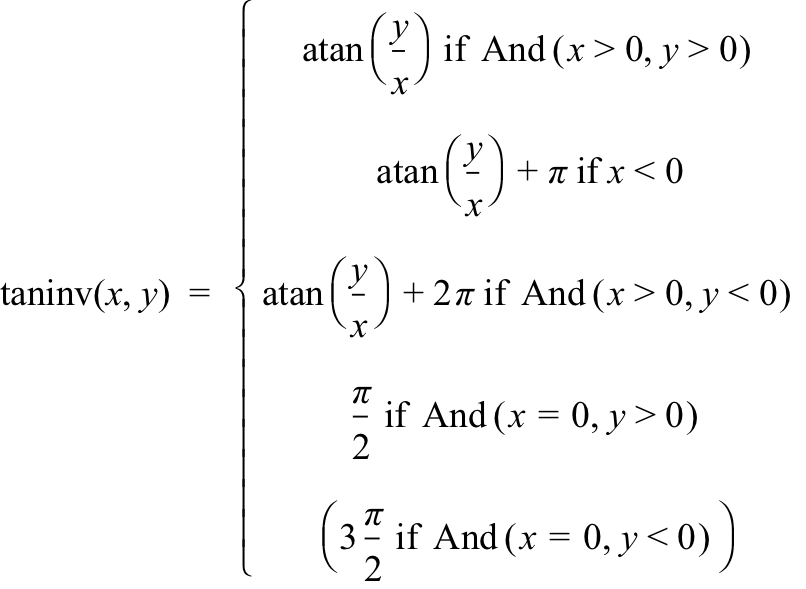
Figure 3.18.8 gives the definition of taninv as it appears in GC (click here for the GC file). The key idea is to pay attention to whether a point’s x-coordinate is positive, negative, or zero.
To do this, type "\taninv\ ctrl-9 x , y =" to start the definition. Type ctrl-shift-A to make the multipart definition. Type ctrl-shift-A to add a new line to the definition.
Test your definition with coordinates having directions (in radians) that you know.
| < Previous Section | Home | Next Section > |