Section 4.1
Constant Rate of Change

The Concept of Differential

We will use the letter "d" preceding a variable to mean that the variable's value "varies a little bit".

The way to envision a differential is to first keep in mind that a variable represents the value of a quantity whose value varies. Variables vary, always.

Another key idea in understanding differentials is that they are variables whose values vary "a little bit". To vary a little bit, they must vary from somewhere. We therefore think of differentials of an independent variable as varying through fixed intervals in the variable's domain.

Finally, a differential is a variable by which another variable varies. This surely sounds confusing. Figure 4.1.1 illustrates this idea. The term "left(x)" in Figure 4.1.1 means the left end of the interval containing the current value of x.

Figure 4.1.1. Variables and Differentials. The value of x varies smoothly through its domain. Differentials in x (dx) are small variations in the variable's value. The symbols "dx" and "$\Delta x$" have different meanings.

Differentials and Constant Rate of Change

The concept of rate of change is foundational to all of calculus. We are unable to give an overview that would convey its significance adequately because this whole book is about rate of change. So we’ll just start.

Suppose that y varies at a constant rate with respect to x. Then $dx$ is a variation (large or tiny) in x as x varies, and $dy$ is a variation in y as the value of y varies in relation to the variation $dx$.

The relationship between variations is $dy=m\cdot dx$ for some number $m,\, m \neq 0$. If the variation in the value of x is a variation from 0, then $dx=x$ and $dy=m\cdot x$.

The value of y when $x=0$ is represented by the letter b, thus $y=b$ when $x=0$.

Therefore, $y=mx+b$ is the general form of the relationship between values of two quantities that vary at a constant rate with respect to each other.

The letter m represents the value of that constant rate of change.

We speak of differentials in two quantities’ measures only when their measures vary at a constant rate with respect to each other.

The letter "d" in "$dy$" means "a little variation in the value of y". Similarly, "$dx$" means "a little variation in the value of x". If k represents the constant rate of change of y with respect to x then $dy=k\cdot dx$. In words, "$dy=k\cdot dx$" means "a little variation in y is k times as large as the variation in x during which $dy$ varies".

Again, we speak of differentials in two quantities’ measures only when the quantities vary at a constant rate with respect to each other over some interval of the independent variable.

Suppose the mass m of a bacterial culture, measured in grams, varied at a constant rate of 5 grams/hr with respect to time, measured in hours, for t hours. This means that within this period, any variation in the culture’s number of grams will be 5 times as large as the variation in the number of hours since measurements began that produced it.

Let $dm$ represent a differential (a varying change) in the culture’s mass during this period, and let $dt$ represent the differential (a varying change) in the number of hours during which $dm$ happens. Then $dm = 5dt$ as the value of $dt$ varies.

1. When $dt$ = 0.1 hours, the mass varied by 0.5 grams during that 0.1 hours, so $dm$ = 0.5 when $dt=0.1$ hours.
2. When $dt=-3.2$ hours, the mass varied by -16 grams during that -3.2 hours, so $dm=-16$ when $dt=-3.2$.
3. When $dt=0.000 001$ hours, the mass varied by 0.000 005 grams during that 0.000 001 hours, so $dm=0.000005$ when $dt=0.000 001$ hours.
4. When $dm=-0.32887321$, we have $-0.3287321=5dt$, so $dt=-0.0657464$ when $dm=-0.3287321$ grams.

Important: All of a-d are necessarily true only under the condition that values of dt are within the period of time that the mass varied at a constant rate of 5 grams/hr.

• "the rate of change of the car’s distance with respect to time", versus

• "the rate of change in the number of miles the car traveled with respect to the number of hours that it traveled"

Exercise Set 4.1

1. Suppose that the measure of quantity A varies at a non-zero constant rate with respect to the measure of quantity B. Is it therefore true that the measure of quantity B varies at a constant rate with respect to the measure of quantity A? Explain.

2. Let c represent the speed of light (299,792.458 km/sec), let D represent the distance a light particle has traveled, and let t represent elapsed time, in seconds.

1. Write the meanings of "$dD$" and "$dt$" in words. (Do not write "dee dee" or "dee tee"!)
2. Note that "d" and "D" have different meanings in "$dD$". What are their respective meanings?
3. What is $dD$ when $dt$ = 0.000 025 sec? Be sure to include the unit of $dD$.
4. What is $dD$ when $dt$= 3.25 sec? Be sure to include the unit of $dD$.
5. e) What is $dt$ when $dD$ = 2 km?
6. What is $dD$ when $dt$ = -0.000 025 sec? What does it mean for $dt$ or $dD$ to have a negative value?

3. A train traveled at a constant speed of 105 km/hr for 0.15 hours. Let s represent the number of kilometers the train traveled and let t represent the number of hours it has traveled.

1. Write the meanings of "$ds$" and "$dt$" in words. (Do not write "dee ess" or "dee tee"!)
2. What is $ds$ when $dt$ = 0.001 sec?
   
3. What is $dt$ when $ds$ is 1.5 km?
4. What is $ds$ when $dt$ = -0.001 sec? What does it mean for $dt$ or $ds$ to have a negative value?

4. A cylindrical tank is 3 m tall with radius 1.5 m. It fills from its bottom by a pipe over a period of 5 minutes. The tank begins partially filled, fills rapidly at first and then slowly. Let V represent the water’s volume in $m^3$, and let h represent the water’s height in meters.

1. The water’s volume does not vary at a constant rate with respect to time. Does the water’s volume vary at a constant rate with respect to its height in the tank? Explain.
2. Explain what $dV$ and $dh$ mean in this context.
3. Express $dV$ in terms of $dh$.
4. When you express $dV$ in terms of $dh$, why is it important that the water’s volume varies at a constant rate with respect to its height?
5. In this situation, how is the meaning of V different from the meaning of $dV$?


One common form of constant rate of change is constant speed, which occurs when variations in a quantity are proportional to variations in time.

For Questions 5 - 7: A car is traveling at a constant speed of 65 miles/hour since entering the highway. Therefore, the number of miles it travels over any period of time at this constant speed is 65 times the number of hours in that period of time.

5. What quantities are y and x in this statement? What are $dy$ and $dx$? State the relationship between $dy$ and $dx$ symbolically.

6. After driving all day a car travels for another 0.3 hours at a constant speed of 65 mi/hr. During that period of time, the number of miles the car traveled that day increases by (65)(0.3) miles. What are y and x in this statement? What are $dy$ and $dx$? What is m?

7. Is there a difference between stating that $y=mx$ and $dy=m\,dx$? Explain in terms of the car’s motion.
   

8. A different car left Phoenix headed toward Los Angeles. It is now traveling at a constant speed of 57 mi/hr. Let y be the car’s number of miles from Los Angeles (not Phoenix) and x be the number of hours driven that day. Which statement about the relationship between y and x is true? Explain.

1. y = mx
2. $dy$ = m $dx$

9. A barrel is being filled with water at the constant rate of 2.5 gal/min. The barrel already had 7 gallons when the spigot opened. Let y be the number of gallons in the barrel and let x be the number of minutes since the spigot opened. Which statement about the relationship between y and x is true? Explain.

1. y = mx
2. $dy$ = m $dx$

10. Suppose that the value of r varies at a constant rate of 3.75 with respect to p.

1. How much will the value of r have varied when the value of p has varied by 6?
2. How much will the value of r have varied when the value of p has varied by 28.3?
3. How much will the value of r have varied when the value of p has varied by -3.1?
4. How much will the value of p have varied when the value of r varied by $-70.3$, ?
5. How much will the value of r have varied when the value of p varied by $\Delta p$?
6. How much does the value of p vary when the value of r varies by $\Delta r$?

11. The value of quantity B varies at a constant rate of 2/5 with respect to variations in the value of quantity A.

1. Determine the values of $dA$ and $dB$ when the value of A varies from:
   
   i) 7 to 13
   
   ii) 258 to 264
   
   iii) -2.5 to 3.5
   
   iv) 4 to 2.3
   
   v) -49 to -50.7
   
   vi) 0.5 to -1.2


2. Exercise 11.a was designed to highlight an important aspect of constant rate of change that was not stated explicitly in this section. What was that aspect of constant rate of change?

12. For each of the scenarios below, express your answer both in words and using mathematical symbols (be sure to define your variables first).

1. Joanne is purchasing fabric. The total cost of the fabric she buys increases at a constant rate of $7.25 per yard of fabric purchased. If she decides to purchase an additional amount of fabric, what can you conclude about the resulting total cost?
2. Between 1990 to 2003, the concentration of carbon monoxide in the atmosphere decreased at a constant rate of 0.248 parts per million per year. What does this mean for the carbon monoxide concentration over a given interval of time in years between 1990 and 2003?
3. Between 1980 and 2004, the number of Medicare enrollees increased at a constant rate of 0.554 million people per year. Given some duration of time in years between 1980 and 2004, what will the result be for the number of Medicare enrollees?

13. A cyclist travels a long stretch of road at a constant speed of 18.4 mph.

1. What two varying quantities are related by constant rate of change in this situation? Define these quantities precisely and thoroughly, including units. (One-word responses are unacceptable, as they will be vague and incomplete!)
2. What two quantities are proportional in this situation?
3. Using the quantities you defined in part a. and/or b , explain the meaning of 18.4 mph as i) a multiplier and ii) a relative size
4. How far will the cyclist travel in 37 minutes? How long will it take the cyclist to go 25 miles? Solve with rate of change reasoning from this section.

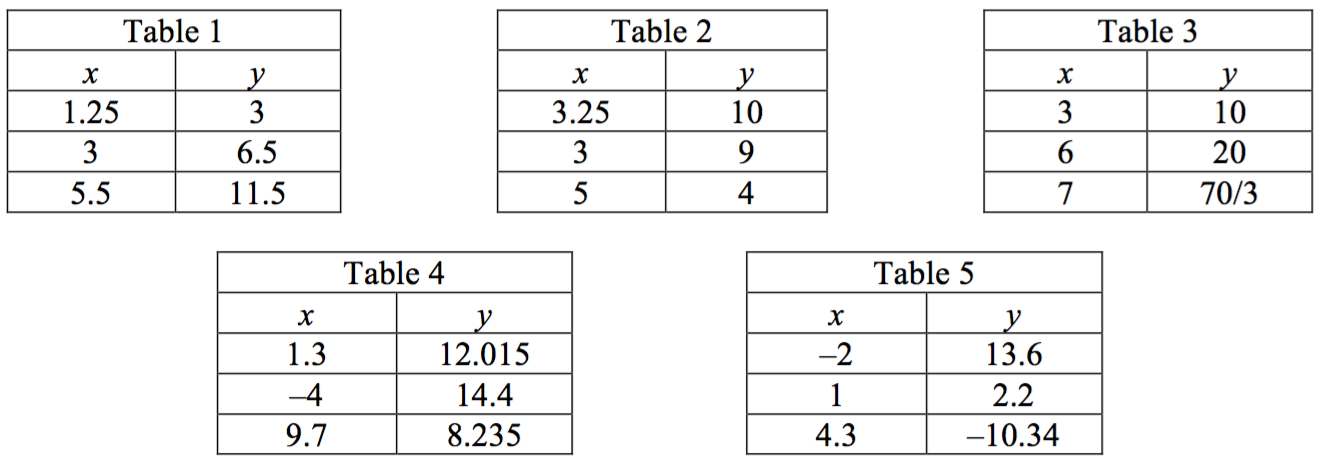
14. Determine which of the following tables' entries are consistent with a claim that x changes at a constant rate with respect to y. State any assumptions you must make to claim that x, in fact, varies at a constant rate with respect to y.

    

15. Two planes took off simultaneously from Phoenix to fly 1870 miles to New York City, flying parallel paths. One plane flew at a constant speed of 510 miles/hour. The second plane at first flew at a constant speed of 420 mi/hr for 3.2 hours.
1. At what constant speed must the second plane fly the remainder of its trip so that the two planes arrive in New York at essentially the same time?
2. Sketch graphs of each plane’s distance from Phoenix versus number of hours flown (assuming they take off and land at the same time). Sketch both graphs on the same axes.

16. Jim can mow a rectangular lawn in 3 hours. Tom can mow the same lawn in 2 hours. They decide to collaborate: They will start at opposite ends and meet somewhere in between.

1. What quantities are involved in this situation?
2. Consider the quantity "fraction of the lawn mowed". Does this quantity vary at a constant rate with respect to time when Jim and Tom work together? If so, at what rate?
3. Use your responses to (a) and (b) to determine the number of hours that Jim and Tom take to mow the lawn when they mow it together.

17. The definition of constant rate of change given above says two quantities vary at a constant rate with respect to each other if variations in their measures are proportional. This is actually imprecise. Suppose an object has a speed of 0 mi/hr.

    1. Is 0 mi/hr a speed? Is 0 mi/hr a constant speed?
    2. Are variations in the number of miles the object travels proportional to the number of hours it has traveled?
    3. Are variations in the number of hours it has traveled proportional to the distance it travels in that number of hours?
    4. Refine the definition of constant rate of change so it accommodates this example.