Section 4.7
Wrinkly Functions

Summation Notation

In this section we will speak of adding large numbers of terms. It will be convenient to represent a sum of many terms without having to write it out. Summation notation was designed to do just that. Instead of writing

1+3+5+7+9+11+13+15+17+19+21+23+25+27+29+31+33+35+37+39

we could instead use a notation that says, in effect, "add up the first 20 odd numbers".

Every odd number can be represented as $2k-1$ for some natural number k. So we will write the above sum as in Figure 4.7.1 and mean the same thing as "add up the first 20 odd numbers".

Read the statement in Figure 4.7.1 as "The sum from k equals 1 to 20 of the numbers represented by $2k-1$." Check that this verbal description matches the long expression given above.

$$\sum_{k=1}^{20} (2k-1)$$ Figure 4.7.1. Summation notation that represents the sum 1+3+…+39.

The summation notation in Figure 4.7.1 expands to $(2\cdot1-1) + (2\cdot2-1) + (2\cdot3-1) + … + (2\cdot20-1)$ as the value of k varies from 1 to 20 in increments of 1.

GC understands summation notation, so using it can be very practical.

A Function That Is a Sum of Many Functions

Sound travels through air as waves of energy formed by variations in pressure caused by something vibrating. Simple sounds are sine waves.

Complex sounds are made by a jumble of simple sounds happening together. When sounds happened together, their pressure waves add to make a complex, bumpy wave.

When graphed relative to time, these complex sound waves have very wrinkly graphs. In this section we will not investigate properties of sound, but we will examine functions that have wrinkly graphs so that you have a better understanding of sound if you study it.

Start with $f(x) = \sin(x)$ and its graph $y = \sin(x)$. The function g defined as $g(x) = (\frac{1}{2})\sin(2x)$ will have half the amplitude of f and twice the frequency—g’s period will be $\frac{1}{2}$ the period of sin(x). Functions f and g are like two simple sounds; the function $(f+g)(x) = f(x)+g(x)$ is like the two sounds happening together for some period of time.

Suppose we combine N sounds $w_0$, $w_1$, …, $w_N$, where sound $w_{k+1}$ has half the amplitude and twice the frequency as sound $w_k$. Suppose also that sound $w_1$ is modeled by sin(x). The function w, below, models the combined sound over time:$$w(x,N) = \sum_{k=0}^{N} {2^{-k}\sin(2^k x)}$$

where x is a measure of time and N is the number of sounds.

Figure 4.7.2 gives a visual perspective on how the function w is made for any value of N. The first animation shows $y = w(x,1)$ being made by adding the next sound wave to $y = w(x,0)$. The second animation shows $y = w(x,2)$ being made by adding the next sound wave to $ y = w(x,1)$. The third animation shows $y = w(x,3)$ being made by adding the next sound wave to $y = w(x,2)$.

Exercise Set 4.7

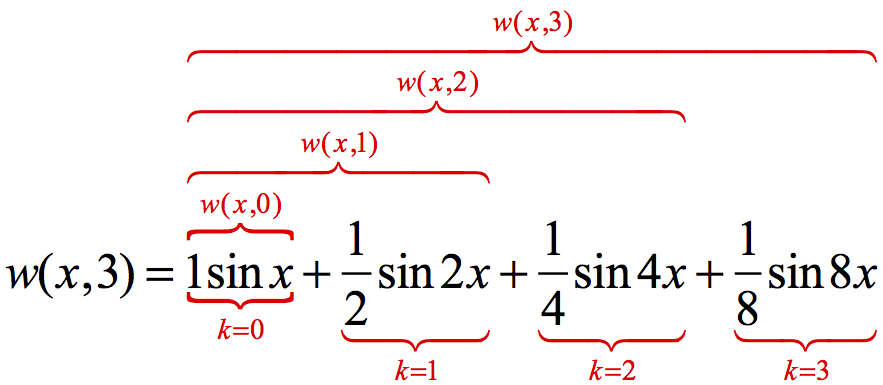
1. First do the following steps:

• Enter the definition of w in GC. Type ctrl-shift-S to get the summation sign: $w(x,N) = \sum_{k=0}^{N} {2^{-k}\sin(2^k x)}$

• Enter $y = w(x, 15)$ on a second line.

• Enter $x = 1.1$ on a third line.

• Zoom in repeatedly around the point where the graphs of $x = 1.1$ and $y = w(x,15)$ intersect. Keep zooming until w appears to have a constant rate of change over the visible x-axis.

Now call the width of the visible x-axis ∆x ("delta x"). What is the value of ∆x? (Trace the graph to see values of x.)