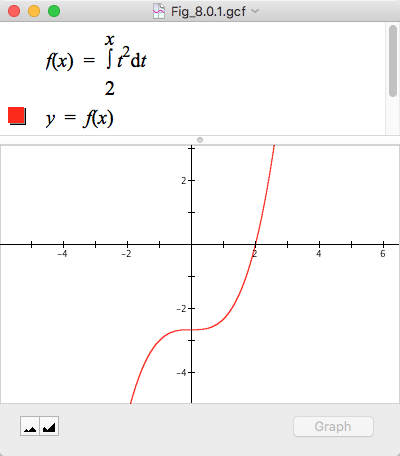
Figure 8.0.1. GC's graph of $y=\int_2^x t^2dt$. Each point on the graph has coordinates $\left(x,\int_2^x t^2dt\right)$.
| < Previous Section | Home | Next Section > |
It will be useful for our future work to review terms and meanings that we established in prior chapters.
| Term |
Symbol | Term's Meaning |
|---|---|---|
| Constant | Number or special symbol | If you intend to represent the value of a quantity whose measure is the same within all situations (e.g., $\pi$), then you are using that notation as a constant. |
| Variable | Any letter at the upper end of the alphabet, such as x, y, or z | If you intend to represent the value of a quantity whose measure varies within a situation, then you are using that letter as a variable. |
| Parameter | Special symbol, such as $\rho$, the symbol for density, or letters near the beginning of the alphabet, such as a, b, c | If you intend to represent the value of a quantity that is constant in a particular situation, but which can vary from one situation to another, then you are using that notation as a parameter |
| Moment of a variable | Any notation that represents a value of a quantity whose value varies | A small interval containing a variable's value. For example,
|
| Incremental change in a variable | $$\Delta x,\Delta y, \Delta t$$ | A fixed-size change in a variable's value. "$\Delta x=0.03$" means that the value of x varied by 0.03 units. |
| Differential change in a variable | $$dx, dy, dt$$ | A varying change in a variable's value, typically varying within an interval of fixed length represented by, for example, $\Delta x, \Delta y, \text{or } \Delta t$. |
| A variable y varies at a constant rate with respect to a variable x | $$y=mx+b$$ |
varies in y are proportional to varies in x. Stated symbolically,$$dy=m\cdot dx$$ for some real number $m$.
If $y=f(x)$ and $f(x)=mx+b$, then $$\begin{align}dy&=f(x+dx)-f(x)\\&=\left( m(x+dx)+b\right)-(mx+b)\\&=(mx+mdx +b)-(mx +b)\\&=m\cdot dx\end{align}$$ |
| Exact rate of change of a function at each moment of its argument | $r_f(x), \dfrac{d}{dx}f(x),\, f'(x)$ |
A function f has an essentially constant rate of change of $r_f(x)$ over a suitably small interval that contains the value of x. To represent an exact rate of change at a specific value of x, such as $x=a$, you could write any of$$r_f(a)\qquad \qquad\left. \dfrac{d}{dx}f(x)\right|_{x=a}\quad \qquad f '(a).$$ |
| Exact net accumulation from exact rate of change | $$\int_a^x r_f(t)dt$$ | Suppose that:
Determining $\int_a^x r_f(t)dt$ from a known rate of change function $r_f$ is called integrating. The function $\int_a^x r_f(t)dt$ is called the integral of $r_f$. In most situations, you do not know the definition of $f$ at the moment that you write a specific form of $\int_a^x r_f(t)dt$ in a particular context. Instead, you will know $r_f$ and $a$. |
| Exact rate of change from exact accumulation | $\dfrac{d}{dx}g(x),r_g(x),g'(x)$ |
Suppose that a known function g gives the exact amount of a quantity in relation to the value x of another quantity. Then:
|
| Antiderivative | ${\displaystyle \int r_g(t)dt}$ | The function g has $r_g$ as its exact rate of change function. Any function $F$ that has $r_g$ as its exact rate of change function (derivative) is called an antiderivative of $r_g$. The function g is an antiderivative of $r_g$ by definition. If $F$ is another antiderivative of $r_g$, then $g(x)=F(x)+C$ for some constant $C$. |
| Closed form definition of a function | A function is defined in closed form if its definition tells us how to compute values of the function in a finite number of operations on values of variables or on values of familiar functions. Notice that we say that a function's definition is in closed form. It is an error to say that a function is in closed form. |
|
| Open form definition of a function | An open form definition of a function is one that gives a conceptual outline of the function’s meaning, but it does not give specific instructions for computing the function’s value in a finite number of steps. The definition of $F$ as $F(x)={\displaystyle \int_1^x t^3dt}$ is in open form. The definition of $F$ as $F(x)=\dfrac{x^4} {4}-\dfrac{1}{4}$ is in closed form. It turns out that these open and closed form definitions of $F$ define the same function--$F(x)$ has the same value in relation to values of x regardless of which definition we use. The open form definition of $F$ tells us explicitly that $F$ is an accumulation function. The closed form definition does not tell us this. But the closed form definition of $F$ does tell us how to compute values $F(x)$ for values of x. |
|
| Unsimplified expression | The expression $x(x-1)(x-2)$ is unsimplified. In simplified form it is $x^3-3x^2+2x$. It is often useful to leave expressions unsimplified, especially when you construct them as models of quantitative situations. The unsimplified expression will remind you of the quantities, relationships, and inferences you made in modeling the situation. A rectangular box of height x, width $2x$, and length $3x+5$ has a volume of $x(2x)(3x+5)$. Leaving the expression unsimplified can remind you of how you came up with the expression. Simplifying this expression as $6x^3+10x^2$ loses the visual reminder that you computed the volume by the conceptual formula $\text{Volume}=\text{height}\cdot\text{width}\cdot\text{length}$. |
The following discussion of the Fundamental Theorem of Calculus (FTC) relies heavily on you having internalized the terms and meanings reviewed in the table given above.
The FTC is fundamental to calculus because it does two things:
It does this by drawing on the fact that rate of change and accumulation are two sides of a coin. When a quantity varies at some rate, the variations accumulate. When a quantity accumulates in relation to variations in another quantity, it varies at some rate with respect to the other quantity.
The FTC's statement is this: Given that $r_f$ is the exact rate of change function for an accumulation function f:
Example: A closed form representation of $\displaystyle{\int_2^x 3e^{-2t}dt}$
Suppose that values of $r_g(x)=3e^{-2x}$ are the exact rate of change of a function g (which we do not know) in relation to all values of x. We know that
$$\int_2^x 3e^{-2t}dt$$
gives the exact net accumulation of g over the interval from $t=2$ to $t=x$ for any value of x.
We also know that any value $g(x)$ is the accumulation of g up to $x=2$ plus the accumulation of g from 2 to x. We say this symbolically as
$$g(x)=g(2)+\int_2^x 3e^{-2t}dt.$$
Although we know neither the definition of g nor the value of $g(2)$, we can say that $$(*)\qquad\int_2^x 3e^{-2t}dt=g(x)-g(2).$$
Unfortunately, without a closed-form definition of g we cannot compute values $g(x)$ directly! Without a closed form definition of g, the best we can do is to approximate values of $g(x)$ numerically for any value of x. GC does this (creates a numerical approximation) when it evaluates $\int_2^x 3e^{-2t}dt$ for any value of x.
However, we can make progress by making a connection between the integral and the notion of antiderivative.
By definition of g, $r_g(x)=3e^{-2x}$ is the exact rate of change function for g, so g is an antiderivative of $r_g(x)=3e^{-2x}$.
But $H(x)=\frac{3}{-2}e^{-2x}$ is also an antiderivative of $r_g(x)=3e^{-2x}$, because $$\frac{d}{dx}\frac{3}{-2}e^{-2x}=3e^{-2x}.$$
Since all antiderivatives of $r_g$ differ by at most a constant, $g(x)=H(x)+C$ for some constant $C$. We therefore have $g(2)=H(2)+C$.
By (*), we now have
$$\begin{align}\int_2^x 3e^{-2t}dt
&=g(x)-g(2)\\[1ex]
&=\left(H(x)+C)\right)-\left(H(2)+C\right)\\[1ex]
&=H(x)-H(2)\\[1ex]
&=\left(\frac{3}{-2}e^{-2x}\right)-\left(\frac{3}{-2}e^{-2\cdot 2}\right)\end{align},$$
We now have a way to compute values of $\int_2^x 3e^{-2t}dt$ directly for any value of x because we have represented values of $\int_2^x 3e^{-2t}dt$ in closed form!
This is what the FTC does for us. Whenever we know a closed form antiderivative of an accumulation function's rate of change function, the FTC enables us to represent the accumulation function (expressed in open form as an integral) in closed form.
Where do antiderivatives come from? They come by recording the rate of change functions produced by closed form representation of accumulation functions. We did this in Chapter 6. We will return to this idea in Section 8.1 and in Chapter 9.
Many books introduce integrals in the context of what they call definite integrals. A definite integral is an integral that has numbers as lower and upper bounds of the integral. The integral $$\int_2^5 t^2dt$$is a definite integral.
If you think of b as a variable, then integrating from a to b is the same as integrating from a to x. The real question then is, "Why use a variable as the upper bound of an integral?"
The answer is that if we define the function f as $f(x)=\int_2^x t^2dt$, then $\int_2^5 t^2dt$ is just $f(5)$. In other words, every value $f(x)$ for a value of x is a definite integral. Figure 8.0.1 is GC's graph of $y=f(x)$ where $f(x)=\int_2^x t^2dt$.
Instead of answering questions that ask for a single number, we can answer questions that request a mathematical model of situations.
A function defined as an integral allows us to answer every question about that situation that requests a definite integral--a single number.

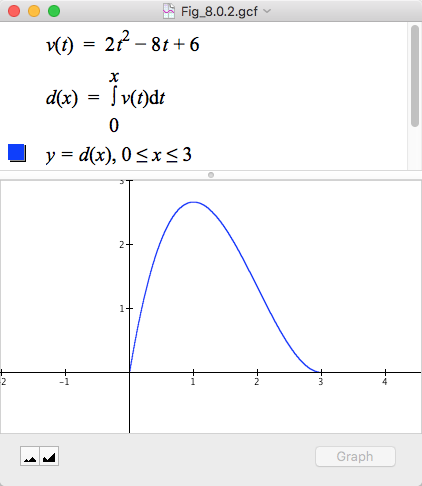
Here is a standard integration problem from another textbook:
A cyclist pedals along a straight road with velocity $v(t)=2t^2-8t+6$ mi/hr for $0\le t \le 3$ hours. How far did the cyclist go in the first hour? In 3 hours? From $t=1$ to $t=3$ hours?
$\dfrac{50}{2.54⋅12⋅5280}$
The Sahara Desert has an area of approximately $9,400,000 \, \mathrm{km^2}$. While estimates of its average depth vary, they center around 150 m. $\mathrm{One \, cm^3}$ holds approximately 8000 grains of sand.
The Grand Canyon is enormous. It is 433 km long and has an average depth of 1.6 km. The US Forest Service estimates its volume at 4.17 trillion $(4.17⋅10^{12}) \, \mathrm{m^3}$. A small dump truck can carry approximately $20.5 \, \mathrm{m^3}$ of sand. Suppose a long line of dump trucks were to dump a load of sand every 30 seconds. Give an unsimplified expression for each of the following quantities' measure:
Essay Question: In the swimming pool context above, a student in another class claimed that p(0.9)−p(0.7)=p(0.2) . Do you agree? Explain why or why not in 2-3 sentences.
The distance that Unser traveled in the first 0.09 hours of the race.
Use function notation to represent the following facts with either an equation or an inequality.
The animation below shows two baseball players, one on 1st base (Player 1) and one on 2nd base (Player 2). Player 1 runs at $18 \mathrm{\frac{ft}{sec}}$. Player 2 runs at $26 \mathrm{\frac{ft}{sec}}$. The distance between bases is 90 ft. The runners leave their bases simultaneously. Assume that they accelerate immediately to their running speeds. Runner 2 stops at 3rd base the moment he reaches it. Runner 1 stops at 2nd base the moment he reaches it.
Define a function B that gives the distance between Player 1 and 2nd base as a function of the number of seconds since they began running. You will need to define your function in two parts (a piecewise function), one part for Player 1’s distance from 2nd base while he is running and another part for the distance after he reaches 2nd base.
Let t be the time in seconds since I started measuring the volume of my bacterial culture in mg. Write down 3 moments at t=1.476:
My investment account's balance increased over a period of 0.25 years from $v(x)=1475$ to $v(x+0.25)=1477$. What is the value of $\Delta x$? What is the value of $\Delta v(x)$?
Last week my investment account grew at a constant rate of 4.73 dollars/day. How many days did it take my account to grow from 1,475 to 1,477?
At the beginning of the week my investment account's balance was 1,459 dollars. If it grows at a constant rate of 4.73/day, what is my account's balance at every point in time during the week? Use $n$ to represent the number of days since the week began.
Identify each function definition as either being of an open form or a closed form. Keep in mind that "$\lim_{x\to0}$" has the same meaning as "when $x \doteq 0$", etc.
Essay Question: Explain the difference between an open form definition of a function and a closed form definition of a function, in your own words.
$f(x)=\mathrm{cos}(x)$ is ______________ of $g(x)=\mathrm{sin}(x)$.
Read the following exchange. Write what you think Bill's final response should be:
Bill: If $d'(4)=14$, that means that at exactly 4 seconds after the ball began rolling down the hill, its instantaneous velocity is $4\mathrm{\frac{m}{s}}$.
Bob: Okay, but what does that velocity mean, exactly?
Bill: Just that! Its velocity at that instant is $4\mathrm{\frac{m}{s}}$. What more do you want?
Bob: If a ball is rolling at a constant velocity, that tells me something. If it's moving at a constant $7\mathrm{\frac{m}{s}}$ I know that $dx=7⋅dt$. I can predict that it goes .7 meters in .1 seconds, and 14 meters in 2 seconds, and $7⋅.218=1.526$ meters in .218 seconds, and generally $7⋅dt$ meters in $dt$ seconds. But your "instantaneous velocity" doesn't help me predict anything about how far it goes.
Bill. Sure it does. It's a velocity, so it has to tell you about how distance varies over time.
Bob: How? As soon as you pick some change in time $dt$, the velocity has changed.
Bill: *thinks for a second, then lightbulb goes on* Ah-ha! Here's how: [finish Bill's statement]
| < Previous Section | Home | Next Section > |