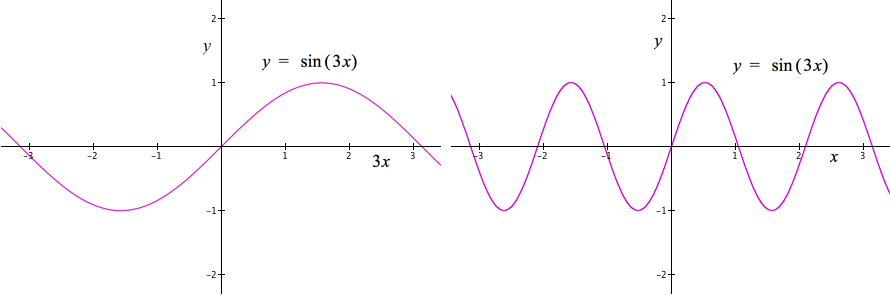
Figure 3.14.1. The period of $\sin(3x)$ with respect to $3x$ is $2\pi$. The period of $\sin(3x)$ with respect to x is $(2/3)\pi$.
| < Previous Section | Home | Next Section > |
When Euler introduced modern function notation in 1734, he stated, "If $f(\frac {x}{a} + c)$ denotes any function of $ \frac {x}{a} + c$ …". His use of parentheses introduced a distinction that we describe today as the distinction between a function’s independent variable and a function's argument.
A function’s argument is the expression that represents the value at which the function will actually be evaluated.
For example, in $y=f(x)$, x is f’s independent variable and x is f’s argument. However, in $y = f(\frac{x}{3} + 5)$, x is f’s independent variable while $\frac{x}{3} + 5$ is f’s argument.
The distinction between independent variable and argument can be very useful. You know that the sine function is periodic with period $2\pi$. This means $\sin(x)=\sin(x+2\pi)$ for all values of x.
However, the sine function has a period of $2\pi$ with respect to what? The sine function has a period of $2\pi$ with respect to its argument. The value of sine begins to repeat any time sine’s argument varies by $2\pi$, as illustrated below.
| x (radians) | $\sin(3x)$ | $\sin(3(x+\frac{2}{3}\pi))$ |
| 0.25 | 0.6816 | 0.6816 |
| 0.4 | 0.9320 | 0.9320 |
| 1.7 | 0.9258 | 0.9258 |
Figure 3.14.1 displays the graph of $y = \sin(3x)$. While it is indeed the case that $\sin(3x)=\sin(3x+2\pi)$, the period of $\sin(3x)$ with respect to x is not $2\pi$. Rather, sine's period with respect to 3x is $2\pi$. Whenever the value of 3x varies by $2\pi$, the value of $\sin(3x)$ repeats itself. However, for the value of $3x$ to vary by $2\pi$, the value of x need only vary by $\frac{2}{3}\pi$.

So $\sin(3x)$ repeats itself whenever the value of $3x$ varies by $2\pi$. How much must the value of x vary so that the value of $3x$ varies by $2\pi$?
The value of $3x$ will vary by $2\pi$ whenever the value of x varies by $\frac{2}{3}\pi$: $$\mathrm{sin} \left(3\left(x+\frac{2}{3}π \right)\right)=\sin\left(3x+3\left(\frac{2}{3}\pi\right)\right)=\sin\left(3x+2\pi\right)$$
Therefore, the value of $\sin(3x)$ is periodic with respect to x, but with a period of $(2/3)\pi$. Whenever the value of x varies by $(2/3)\pi$, the value of $3x$ varies by $2\pi$, and therefore the value of $\sin(3x)$ repeats itself whenever the value of x varies by $(2/3)\pi$.
We can express the above reasoning formally. The value of $\sin(ax+b)$ repeats itself whenever $ax+b$ varies by $2\pi$. In other words, if we let $\Delta x$ represent the variation in the value of x that results in the value of $ax+b$ varying by $2\pi$, then $a(x+\Delta x)+b=(ax+b)+2\pi$. Solving for $\Delta x$, we get:
$$\begin{align}a(x+\Delta x)+b&=(ax+b)+2\pi\\[1ex] ax+a\Delta x+b&=(ax+b)+2\pi\\[1ex] (ax+b)+a\Delta x&=(ax+b)+2\pi\\[1ex] a\Delta x&=2\pi\\[1ex] \Delta x&=\frac{2\pi}{a}\end{align}$$
Therefore, the period of $\sin(ax+b)$ with respect to x is $\dfrac{2\pi}{a}$. Whenever the value of x varies by $2\pi/a$, the value of $ax+b$ varies by $2\pi$.
| < Previous Section | Home | Next Section > |