Section 3.18
Inverse of a Function

A graph of a relationship between two variables x and y actually shows two relationships. It shows values of y that are related to values of x, and it shows values of x that are related to values of y.

Figure 3.18.1 illustrates the two perspectives on what a graph shows us, and the difference between perspectives is in which variable you take as the independent variable and in the flexibility of seeing independent variables on either horizontal or vertical axes.

Figure 3.18.1 shows that even though we start with y as a function of x, and define the relationship with $$f(x)=3x+2,$$ we could just as easily look at the graph as showing x as a function of y, with the relationship defined as $$g(y)= \frac{y-2}{3}.$$

We also can see inverse relationships in non-graphical settings. The formula for converting a temperature in degrees Fahrenheit (F°) to a an equivalent temperature in degrees Celsius (C°) is $y = \frac{5}{9}(x‑32)$, where x is a temperature in F° and y is a temperature in C°.

Suppose you are in France, where all temperatures are in degrees Celsius! How do you go the other way, from C° to F°? You must solve for x in terms of y (Figure 3.18.2).

Figure 3.18.2. Start with an equation that gives y, a number in degrees C, in terms of x,a number in degrees F; end with an equation that gives x, a number in degrees F, in terms of y, a number in degrees C.

If we call the original function in Figure 3.18.2 f, then $$f(x) = \frac{5}{9}(x‑32).$$

If we call the end function in Figure 3.18.2 g, then
$$g(y) = \frac{9}{5}y + 32.$$
The function f converts x degrees Fahrenheit to y degrees Celsius. The function g converts y degrees Celsius to x degrees Fahrenheit.

Suppose we start with 82 degrees F, convert it into $y_0$ degrees C, and then convert $y_0$ degrees C back to $x_0$ degrees F? What should $x_0$ be? 82! Indeed, if we convert any temperature x degrees F to y degrees C, then convert y degrees C back to a number of degrees F, that number should be the value we started with. We can express this symbolically as $$g(f(x))= x.$$

The same will be true about converting from degrees C to degrees F and back to degrees C. After all the converting, we should end with the temperature in degrees C that we start with. We can express this symbolically as $$f(g(y))=y.$$

Reflection 3.18.1: Convince yourself that with f and g defined as above, $f(g(17))=17$ and that $g(f(85))=85$. Question: What is the unit for both instances of 17 in $f(g(17))=17$? What is the unit for both instances of 85 in $g(f(85))=85$?

Reflection 3.18.2: Let f and g be as in the Celsius $\leftrightarrow$ Fahrenheit example. In the statement $f(g(y)) = y$, what is the unit of y? In the statement $g(f(x)=x$, what is the unit of x?

Reflection 3.18.3: Let f and g be as in the Celsius $\leftrightarrow$ Fahrenheit example. Would it be a valid statement to say $f(g(u))=u$ or $g(f(v))=v$ for real numbers u and v? In other words, must we use x and y?

Inverse Functions

The idea of inverse functions is a generalization of the Celsius $\leftrightarrow$ Fahrenheit example.

When a function h has an inverse function, it is represented as $h^{-1}$ (read "h inverse"). The "-1" in $h^{-1}$ is not an exponent. Rather, it is the general symbol for undoing what something does.

If h and k are inverse functions, then $h=k^{-1}$ and $k = h^{-1}$ ("h equals k inverse and k equals h inverse"). The function $h^{-1}$ undoes what the function h does to values of its independent variable. The function $k^{-1}$ undoes what the function k does to its independent variable.

Every Function Has an Inverse, but Not Every Inverse is a Function

Suppose that j is a function with w as its independent variable and z as its dependent variable. The inverse of j, namely $j^{-1}$, would have z as its independent variable and w as its dependent variable.

If j relates two values of w to one value of z, then the inverse of j will not be a function. If, for example, $j(2)=7$ and $j(3)=7$, then $j^{-1}(7)$ could be 2 or it could be 3. This means that $j^{-1}$ could not be a function because $j^{-1}(7)$ does not have a unique value.

Inverse Trigonometric Functions

Problem: A construction company has contracted to design and build a highway on-ramp similar to the one in Figure 3.43. The on-ramp must carry cars from street level to highway level, a height of 50m, make a turn of $\frac{3π}{2}$ radians, or 270°, and have a radius of 120 m. They need to determine the angle of elevation (angle from parallel to ground) that the on-ramp must make at all points along it so that the end of the on-ramp meets the highway it will join.

Solution and reasoning:

• The length of the on-ramp will be $$\frac{3π}{2}(120) \space \mathrm{meters},$$ or 180π meters. To think about angle of elevation, imagine that the on-ramp will be straight, making a triangle that is 50m high and has a hypotenuse of 180π m (Figure 3.18.4).
• We know that $\sin(θ)= \dfrac{50}{180}π$, but we need to know θ, not sin(θ). We need an inverse function for sin(θ). GC has a builtin inverse sine function. It is named asin (pronounced "a-sine"). "asin" is short for "arcsine", which itself is shorthand for "the arc (in radians) that produces a sine" of the desired value.
• Enter $\mathrm{asin}\left(\dfrac{50}{180}π\right)$ into GC and it will report that $$\asin\left(\frac{50}{180}π\right)=0.088535 \space \text{(to 6 significant digits)}.$$
• This means that the sine of an arc whose measure is 0.088535 radians will be $\dfrac{50}{180}\pi$.
• So the construction company must build short sections of the on-ramp so that at every point along each section, the section's angle of elevation from horizontal is 0.088535 radians, or 5.072684 degrees. If they do that, their on-ramp of length 180π m will rise 50 m from street level to meet the highway.

Figure 3.18.4. The on-ramp straightened out. It must have an angle of elevation of θ radians so that a car rises 50 m as it drives 180π (565.489) m along it.

The matter of inverse functions of trigonometric functions is tricky, because trigonometric functions are not one-to-one over the domains of their independent variables (Figure 3.18.5).

Figure 3.18.5. GC displays of the graphs of y=sin(x) [top], y= cos(x) [middle], and y = tan(x) [bottom], each with the graph of y = 0.5 overlaid on it.

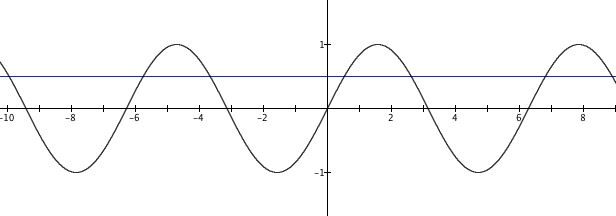
Each function in Figure 3.18.5 has an infinite number of values that produce a value of 0.5. It will therefore not be possible to define an inverse function for any of them. However, we can restrict the domain of each function to an interval over which it is one-to-one. For example, Figure 3.18.6 shows the domain of sine’s independent variable restricted to the interval $-\frac{π}{2}$ to $\frac{π}{2}$. Over this interval, sin(x) is one-to-one and therefore has an inverse function.

Figure 3.18.6. Domain of sine’s independent variable restricted to $-\frac{π}{2}\leq x \leq \frac{π}{2}$. Over this interval, f(x)=sin(x) is one-to-one and therefore has an inverse function.

The function is one-to-one when independent variable restricted to $-\frac{π}{2} ≤ x≤\frac{π}{2}$. So sin(x) has an inverse over that interval.

The inverse of sin, called arc sine ("asin" in GC), is defined as $$\mathrm{asin}(y)=x\text{ such that }\sin(x)=y.$$ This might seem like a strange definition, but it is not. The graph in Figure 3.14.1 came from $y = \sin(x)$, so our computing devices have a method to compute sin(x).

We define asin conceptually, saying to reverse the process of assigning values to sin(x), whatever that process is.

You will learn methods for computing approximations to sin(x) and asin(y) in Calculus II. Your calculator and GC have these methods programmed into them.

For the meantime, celebrate the fact that your calculator has a magical button labeled $\sin^{-1}$ and that GC has a magical function named asin.

Reflection 3.18.4. Examine a displayed graph of $y = \cos(x)$ in GC. How could you restrict its independent variable to an interval so that cos is one-to-one over that interval? There is more than one way to do this; try to make it symmetric around 0 or as closely tied to 0 as possible.

Reflection 3.18.5. Examine a displayed graph of $y = \tan(x)$ in GC. How could you restrict its independent variable to an interval so that tan is one-to-one over that interval? There is more than one way to do this; try to make it symmetric around 0 or as closely tied to 0 as possible.

Converting from Cartesian Coordinates to Polar Coordinates

There will be occasions when you need to convert from rectangular coordinates to polar coordinates.

A point’s distance from the pole is easy. If the point P has rectangular coordinates (a, b), denoted hereafter as P:(a, b), then, by the Pythagorean Theorem, $r= \sqrt{a^2+b^2}$. Or, defined as a function, if a point has coordinates (x, y), then the point’s distance from the pole is $r(x,y)= \sqrt{x^2+y^2}$.

Determining a point's angle from the reference direction (the positive x-axis) is a bit trickier than determining its distance from the origin.

As illustrated in Figure 3.18.7 (a), if P:(a, b) is in the 1st or 4th quadrant, then the angle from the reference direction has a measure of $\atan(b/a)$.

Figure 3.18.7 (a). If a point with coordinates $(a,b)$ is in the first or fourth quadrant,
its direction from the positive x-axis is $\atan(b/a)$.

However, there are two problems in determining a point's direction from the positive x-axis. The first problem arises when the point is is in the coordinate plane's 2nd or 3rd quadrant. The second problem arises when the point is on the y-axis.

Figure 3.18.7 (b) illustrates the first problem. It shows two points, $Q:(-1.75,-1.25)$ and $P:(1.75,1.25)$. The quotient of point Q’s coordinates is the same as the quotient of P’s coordinates, so the atan function cannot distinguish between points Q and P in terms of their direction from the positive x-axis.

Figure 3.18.7 (b). If a point with coordinates $(a,b)$ is in the 3rd quadrant, the quotient of its coordinates will be the same as the point having coordinates $(-a,-b)$ in the 1st quadrant. The quotient of the points' coordinates will be the same, and therefore $\atan(a,b)$ and $\atan(-a,-b)$ will have the same value.

Figure 3.18.7 (c) shows a similar problem distinguishing between the direction of point $R:(-1.75,1.25)$ in the second quadrant from the direction of point $S:(1.75,-1.25)$ in the fourth quadrant. The quotient of S's coordinates is the same as the quotient of R’s coordinates.

Figure 3.18.7 (c). If a point with coordinates $(a,b)$ is in the 2nd quadrant, the quotient of its coordinates will be the same as the point having coordinates $(-a,-b)$ in the 4th quadrant. The quotient of the points' coordinates will be the same, and therefore $\atan(a,b)$ and $\atan(-a,-b)$ will have the same value.

In short, atan cannot distinguish between directions of points $(a,b)$ and $(-a,-b)$, nor can atan distinguish between directions of points $(a,-b)$ and $(-a,b)$.

The second problem arises if a point is on the y-axis. The function $\atan(\theta)$ (arctangent $\theta$) is defined only for values of $\theta$ such that $-\dfrac{\pi}{2}\lt \theta \lt \dfrac{\pi}{2}$. It is not defined for $\theta= \dfrac{\pi}{2}$ (when a point is on the positive y-axis) or for $\theta= -\dfrac{\pi}{2}$ (when a point is on the negative y axis).

A solution to both problems is to define a new function that we call taninv (tangent inverse). It will have two independent variables: the point’s x-coordinate and the point's y coordinate.

Any value $\taninv(x,y)$ will be a point’s direction from the positive x-axis, given as an angle measure in radians between 0 and $2\pi$.

Figure 3.18.8 gives the definition of taninv as it appears in GC (click here for the GC file). The key idea is to pay attention to whether a point’s x-coordinate is positive, negative, or zero.

• If $x > 0$ and $y > 0$, then atan($y/x$) gives the correct direction (see Figure 3.18.7).
• If $x > 0$ and $y < 0$, then atan$(y/x)$ will give a result between $-\pi/2$ and 0, so add $2\pi$ to give a result between $3\pi/2$ and $2\pi$.
• If $x < 0$, then the direction given by atan($y/x$) is off by a rotation of $\pi$ (see Figure 3.18.7), so add $\pi$ to the value of atan($y/x$).
• If $x=0$ and $y > 0$, the point is on the positive y-axis.
• If $x=0$ and $y < 0$, the point is on the negative y-axis.
• You should notice that taninv(0,0) is undefined. This makes sense because the point (0,0) does not have a direction from (0,0).

Exercise Set 3.18

1. Enter $y= \sin(x), 0 ≤ x < 2\pi$ into GC. The point $(1.2, 0.9320391)$ is on the graph of $y = \sin(x)$. To what point on the graph of $y = \sin(\sqrt{x})$ is $(1.2, 0.9320391)$ shifted? Justify your answer.


2. Enter $y = \sin(\sqrt{x}), x ≥ 0$ into GC. The point $(6, 0.6381576)$ is on its graph. What point on the graph of $y = \sin(x)$ is shifted to the point $(6, 0.6381576)$ on the graph of $y = \sin(\sqrt{x})$? Justify your answer.


3. Enter $y = \cos(x)$ into GC. The point $(0.8, 0.69670671)$ is on the graph of $y = \cos(x)$. What point on the graph of $y = \cos(3x - 2)$ is it shifted to? Justify your answer.


4. Enter $y = \sec(x)$ in GC. This will display a graph of the secant function. Examine its graph. How could you restrict its independent variable to an interval so that sec is one-to-one over that interval? There is more than one way to do this; try to make it symmetric around 0 or as closely tied to 0 as possible.


5. Enter $y = \csc(x)$ in GC. This will display a graph of the cosecant function. Examine its graph. How could you restrict its independent variable to an interval so that csc is one-to-one over that interval? There is more than one way to do this; try to make it symmetric around 0 or as closely tied to 0 as possible.


6. Enter the definition of taninv (Figure 3.18.8) in GC.

To do this, type "\taninv\ ctrl-9 x , y =" to start the definition. Type ctrl-shift-A to make the multipart definition. Type ctrl-shift-A to add a new line to the definition.

Test your definition with coordinates having directions (in radians) that you know.



7. After completing Exercise 3.18.6, enter taninv(0,0). GC will display "not a number". This is GC’s way of saying that taninv(0,0) is undefined.
1. Why is it reasonable that taninv(0,0) should be undefined? What would it mean were taninv(0,0) = 1?
2. What is it about the definition of taninv that keeps GC from giving a value for taninv(0,0)?


8. The following are points' coordinates in the polar system. Convert them from polar coordinates to rectangular coordinates.
1. $(3,2)$
2. $(-4,-1)$
3. $(\sqrt 7,\sqrt 7)$
4. $(0,5)$


9. The following are points' coordinates in the rectangular system. Convert them from rectangular coordinates to polar coordinates.
1. $(3,2)$
2. $(-4,-1)$
3. $(\sqrt 7,\sqrt 7)$
4. $(0,5)$
10. A jet car will try for a new world speed record. Your job is to videotape the car as it makes its run. You can program your motorized camera tripod with a function to aim the camera in particular directions at particular moments in time. The car will approach your station at a speed of 972 $\mathrm{\frac{km}{hr}}$. Your camera will start when the car breaks a laser beam 10 km away going full speed. The tripod will be 200 m from nearest point of the car’s path. Define a function that will aim the camera in the proper direction so that it remains pointed at the car as it travels past your camera and beyond.






11. The functions sin and asin are inverse functions. The figure below contains GC’s displays of $y = \sin(\mathrm{asin}(x))$ and $y = \mathrm{asin}(\sin(x))$. Explain why these graphs appear as they do.





12. One mile is 1.62 km and one mile is 5280 feet.
1. Define a function f so that $f(x)$ gives the number of meters per second that is equivalent to x miles per hour. You should get $f(22)=9.9$.
2. Define a function g so that $g(x)$ gives the number of feet per second that is equivalent to x meters per second. You should get $g(20)=65.6168$ (to 7 significant digits).
3. Define a function h so that $h(x)$ gives the number of miles per hour that is equivalent to x meters per second. Why is it true that if you define h correctly, the graph of $y=h(f(x))$ is the same as the graph of $y=x$?
4. Define a function k so that $k(x)$ gives the number of meters per second that is equivalent to x feet per second. Why is it true that if you define k correctly, the graph of $y=k(g(x))$ is the same as the graph of $y=x$?