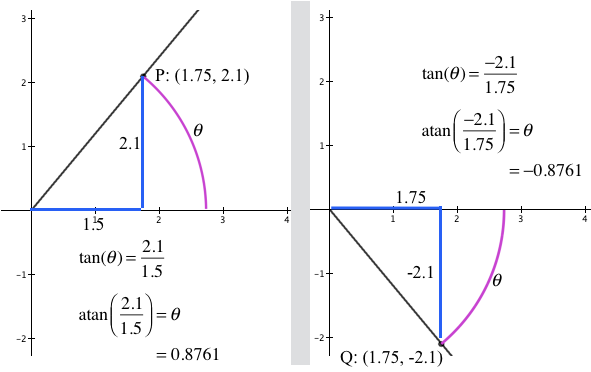
Figure 11.2.1 (a). If a point with coordinates $(a,b)$ is in the first or fourth quadrant,
its direction from the positive x-axis is $\atan(b/a)$.
| < Previous Section | Home | Next Section>> |
There will be occasions when you need to convert from rectangular coordinates to polar coordinates.
A point’s distance from the pole is easy. If the point P has rectangular coordinates (a, b), denoted hereafter as P:(a, b), then, by the Pythagorean Theorem, $r= \sqrt{a^2+b^2}$. Or, defined as a function, if a point has coordinates (x, y), then the point’s distance from the pole is $r(x,y)= \sqrt{x^2+y^2}$.
Determining a point's angle from the reference direction (the positive x-axis) is a bit trickier than determining its distance from the origin.
As illustrated in Figure 11.2.1 (a), if P:(a, b) is in the 1st or 4th quadrant, then the angle from the reference direction has a measure of $\atan(b/a)$.

However, there are two problems in determining a point's direction from the positive x-axis. The first problem arises when the point is is in the coordinate plane's 2nd or 3rd quadrant. The second problem arises when the point is on the y-axis.
Figure 11.2.1 (b) illustrates the first problem. It shows two points, $Q:(-1.75,-1.25)$ and $P:(1.75,1.25)$. The quotient of point Q’s coordinates is the same as the quotient of P’s coordinates (approximately 0.7142857), so the atan function cannot distinguish between points Q and P in terms of their directions from the positive x-axis.
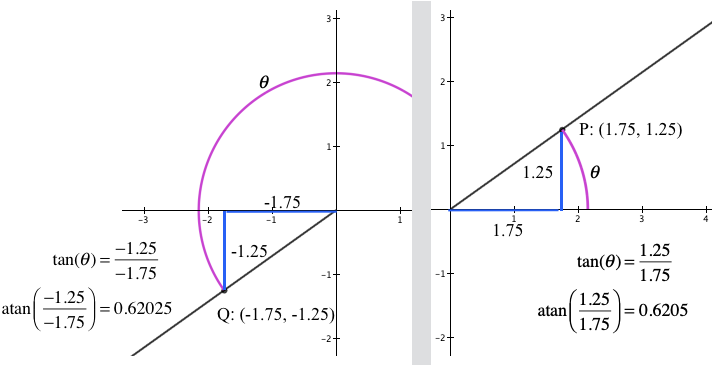
Figure 11.2.1 (c) shows a similar problem with using atan to distinguish between the direction of point $R:(-1.75,1.25)$ in the second quadrant from the direction of point $S:(1.75,-1.25)$ in the fourth quadrant. The quotient of S's coordinates is the same as the quotient of R’s coordinates. The value of $\atan\left(\frac{1.25}{-1.75}\right)$ is the same as the value of $\atan\left(\frac{-1.25}{1.75}\right)$ because both quotients are equal to $-\frac{1.25}{1.75}$.
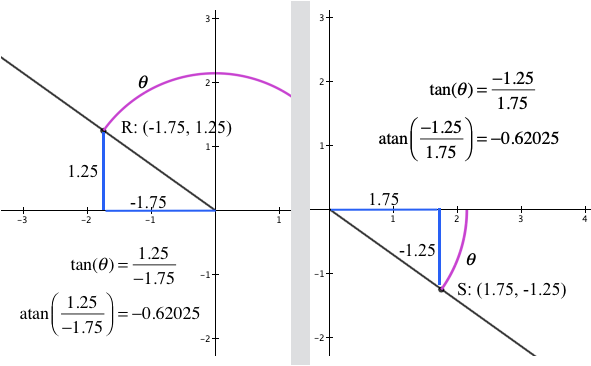
In short, atan cannot distinguish between directions of points $(a,b)$ and $(-a,-b)$, nor can atan distinguish between directions of points $(a,-b)$ and $(-a,b)$.
The second problem arises if a point is on the y-axis. The function $\atan(\theta)$ (arctangent $\theta$) is defined only for values of $\theta$ such that $-\dfrac{\pi}{2}\lt \theta \lt \dfrac{\pi}{2}$. It is not defined for $\theta= \dfrac{\pi}{2}$ (when a point is on the positive y-axis) or for $\theta= -\dfrac{\pi}{2}$ (when a point is on the negative y axis).
A solution to both problems is to define a new function that we will call taninv (tangent inverse). It will have two independent variables: the point’s x-coordinate and the point's y coordinate.
Any value $\taninv(x,y)$ will be a point’s direction from the positive x-axis, given as an angle measure in radians between 0 and $2\pi$.
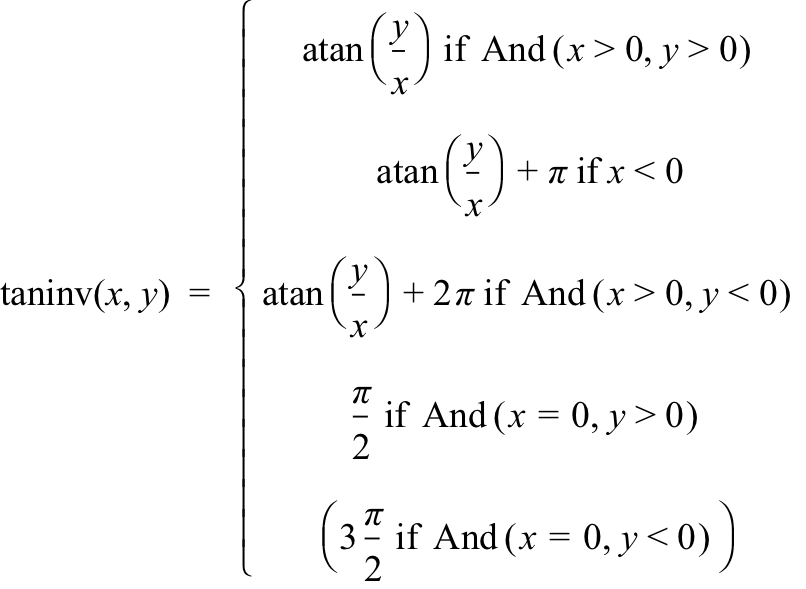
Figure 11.2.2 gives the definition of taninv as it appears in GC (click here for the GC file). The key idea is to pay attention to whether a point’s x-coordinate is positive, negative, or zero.
The key idea in converting from polar to rectangular coordinates is that, in the unit circle, any point on the circle has coordinates $(\cos\theta,\sin\theta)$ where $\theta$ is the measure of the angle made by the point, (0,0), and the positive x-axis (Figure 11.2.3).
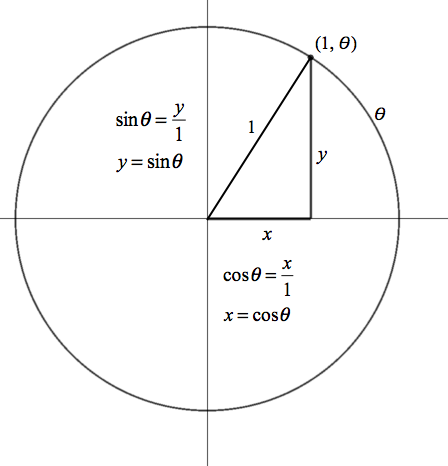
Figure 11.2.3. Polar coordinates $(1,\theta)$ converted to rectangular coordinates $(\cos\theta,\sin\theta)$.
The rectangular coordinates of points not on the unit circle will simply be the rectangular coordinates of the corresponding point on the unit circle, scaled by the point's distance from the origin (Figure 11.2.4)
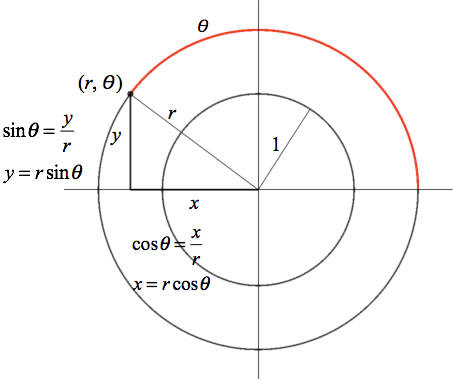
Figure 11.2.4. Polar coordinates $(r,\theta)$ converted to rectangular coordinates $(r\cos\theta,r\sin\theta)$.
To do this, type "\taninv\ ctrl-9 x , y =" to start the definition. Type ctrl-shift-A to make the multipart definition. Type ctrl-shift-A to add a new line to the definition.
Test your definition with coordinates having directions (in radians) that you know.
| < Previous Section | Home | Next Section>> |