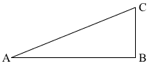
Figure 2.2.1. A right triangle
| < Previous Section | Home | Next Section > |
What are you measuring when you measure an angle?
What does it mean that an angle has a measure of 37.2 degrees?
Answers to these questions are at the heart of trigonometry and trigonometric functions.
In school, you learned a statement like this: Given right triangle ABC, $$\sin(A)=\mathrm{\dfrac{opposite}{hypotenuse}}$$
Notice that in the above formulation, "A" is the name of an angle. It is not a the measure of angle A. It is not a number. Because A in sin(A) is not a number, the pair $\left(A,\sin(A)\right)$ cannot be plotted in a coordinate system to make a graph.

For sine to be a function, you must think of "A" in sin(A) as the measure of an angle and not the name of an angle. Then, inputs to sine, cosine, etc. are numbers, not geometric figures.
You also must think of sine, cosine, etc. as functions of angle measures. To do this you must be able to envision how an angle’s measure varies. The following animations show two ways of thinking about how an angle’s measure might vary.
In Figure 2.3, the measure of angle A varies by making BC longer. BC getting longer makes the measure of angle A increase, and it also increases the length of AC, the hypotenuse. Move your pointer away from the animation to make the control bar disappear.
There are three problems with this way of envisioning angle A’s measure varying:
A better way to envision the measure of angle A varying is to place C on a circle centered at A with radius AC. Then let C travel along the circle. Figure 2.4 shows this.
Reflection 2.2.1: Compare Figures 2.2.2 and 2.2.3. They both show angle A varying in size. How do they differ in the way angle A varies? How might the way you envision angle A varying matter?
There are many advantages to thinking about an angle’s measure varying by moving a vertex of the triangle along a circle. One is that the triangle's hypotenuse stays the same length.
We can therefore make a right triangle’s hypotenuse the unit of arc length, measuring everything else in terms of that length.
Another advantage is that the triangle’s hypotenuse is the circle’s radius. This means that we can measure angles by measuring the length of arc on a circle that they subtend. The arc is measured in units of the circle’s radius.
The following animation shows a circle’s radius being moved to the circle. The circle’s radius then becomes an arc that has a length 1 radius. As the arc varies, the angle that subtends that arc varies. The number of radii subtended is the measure of the angle that subtends it. Note: The angle varies because the the length of the arc that it subtends varies.
Reflection 2.2.2: What does it mean for the red line in Figure 2.5 to move from the circle’s radius to the circle itself? What does this have to do with measuring angles?
Reflection 2.2.3: What do the numbers around the circle mean? What do the tick marks along the circle mean?
Start with an angle. Imagine a circle centered at the angle's vertex. The angle’s measure is the length of the arc the angle subtends, measured in units of the circle’s radius.
You now have a way to think of an angle’s measure varying systematically. The measure increases from 0 to 2π radii—and then everything repeats.
We can now say what x represent in the graph of $y = \sin(x)$. It represents an arc length, measured in units of a circle’s radius.
When an arc on a circle is measured in units of the circle’s radius, the measure is said to be in radians. We will measure angles in radians throughout this book.
We put an arc length that is on a circle onto an axis by rolling the circle along a line. Think of the circle as being made of an infinitely long thread that is tied to (0,0). As the circle rolls, the thread unravels to leave a length that is the length of arc that has rolled along the axis. See the animation in Figure 2.6.
Zero (0) radians means that none of the circle’s circumference has been rolled onto the axis; 1 represents having rolled the length of the circle’s radius onto the axis. The number 1 on the axis therefore represents 1 radian of arc on the unit circle. This is made clearer in Figure 2.2.6. The circle has tick marks that are 0.25 radii apart. As the circle rolls, it deposits tick marks onto the axis. This is how to imagine getting measures of arc from a circle onto a horizontal axis.
We can now say the meaning of x in $y = \sin(x)$. The letter x represents an angle measure, where any angle measure is the length of arc on a circle the angle subtends, measured in the circle's radius. So, "1" on the x-axis represents an arc length of 1 radius on a circle that has that length as its radius. "3.75" on the x-axis represents an arc length of 3.75 radius lengths on a circle with a radius of 1. Notice: Every circle can be considered a unit circle. Every circle has a radius of 1 radius.
Draw two circles with radii of different lengths. Highlight arcs on each of lengths 1, 0.5, 3.75, and 5.5 radii. Do these arcs on the two circles determine equivalent angles?
The text mentioned repeatedly that the unit of measure for arc length on a circle is the length of one radius. Suppose a circle’s radius is 5 inches. Can you still measure arcs on the circle in units of 1 radius?
Ron jogged around a circular lake. The lake has a diameter of 3 miles. Ron stopped to rest after running 5 miles. Imagine an angle formed by Ron’s starting point, the lake’s center, and his resting point. What is the measure of this angle in radians?
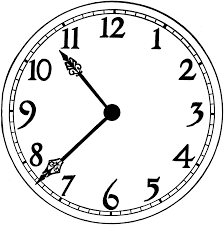
The clock face below shows a time of 10:38. What is the counter-clockwise measure of the angle formed by the minute and hour hands, measured going from the hour hand to the minute hand? Going from the minute hand to the hour hand?
Is an angle measure of 0 radians the same as an angle measure of 2π radians? Explain.
The minute hand of a clock moved from 12 minutes past an hour to 51 minutes past the same hour. What is the radian measure of the angle through which it moved?
| < Previous Section | Home | Next Section > |