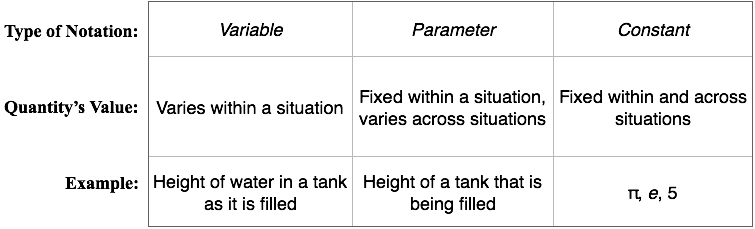
Figure 3.1.2. Types of notation and their meanings. What a notation means depends on what you intend it to represent.
| < Previous Section | Home | Next Section > |
Whether a mathematical notation is a variable, parameter, or constant depends on what you mean by it.
Examine the cylinders depicted in Figure 3.1.1. They are partially filled with water. As they sit, it appears that nothing about the cylinders or water in them varies. Now imagine that each cylinder is being filled from a pipe at its bottom. Then the water’s height in each cylinder varies.
If we let $h_1$, $h_2$, and $h_3$ represent the water’s height in the respective cylinders and imagine that each height varies, then the values of $h_1$, $h_2$, and $h_3$ vary as the water’s height varies within its cylinder. Play the animation in Figure 3.1.1 to see what you envisioned. Move your cursor away from the animation to make the control bar disappear.
Figure 3.1.1. $h_1$, $h_2$, and $h_3$ represent the height of the water in the three cylinders, respectively. Each variable's value varies as the water’s height varies. $r$ and $H$ are parameters. Their values are constant for each tank, but their values vary across tanks.
Some quantities in Figure 3.1.1 do not vary within a cylinder but vary across cylinders. Any cylinder’s radius does not vary, nor does its height, nor does the area of its water’s exposed surface. For each cylinder, its water’s height and volume do vary. So if we let r represent a cylinder’s radius, the value of r, for each cylinder, does not vary. But the value of r varies across cylinders. Similarly, if we let H represent a cylinder’s height, the value of H, in each cylinder, does not vary. But the value of H varies across cylinders.
Again, when we say that a notation has the meaning of a variable, we mean that it represents the value of a quantity whose value varies within a situation. When we use a notation to represent a value that is constant in a situation but which can vary from one situation to another, we are using the notation as a parameter. We mean that the notation represents the value of a quantity that is constant within a situation, but the quantity could have different values in different situations.
By convention, we will use the term domain to refer to the set of values that a variable can have. If in Figure 3.1.1 we use b to represent the initial height of water in a cylinder, then the domain of $h_i$ for any of i = 1, 2, or 3, is b ≤ $h_i$ ≤ H.The letters b, r, and H are used as parameters. The letters $h_1$, $h_2$, and $h_3$ are used as variables.
In this textbook, we will assume that the domain of any variable is the set of real numbers unless stated otherwise or unless restricted by context.
We also can speak of a variable’s value varying in the absence of a specific quantity. When we say something like, "The value of x varies between 2 and 5", we are actually saying that there is some yet-to-be-known quantity lurking in the background whose measure varies from 2 to 5, passing through all real numbers between 2 and 5.
Values that do not vary are called constants. Some constants are universal, like π and e. Their values do not depend on a particular context. Other constants are constant only with respect to a situation. In the statement, "Billy has 5 toys. His father gave him 2 more. He has 5+2 toys altogether", the number of toys Bill started with and the number of toys he received are constants.
In the statement, "Billy has m toys. His father gave him n more. He has m+n toys altogether", the number of toys he started with and received are constants within the situation. But they are expressed generally. This means that the statement is given with the intention that we are describing many potential situations. The statement " m+n" says what to do with those numbers once they are known. The letters "m" and "n" are used as parameters.
Figure 3.1.2 summarizes the distinctions among variables, parameters, and constants.

This ambiguity in uses of "change" can lead to misreading or misinterpreting a statement about "change in x" or "change in y". Does the person or textbook mean change in progress, completed change, or replacing one value by another?
Our uses of "vary", "variation", and "change" is not a rule for you to follow. However, it is important that you be aware of which meaning of "change" you have in mind or someone else intends when using it.
The word "change" in the phrase "rate of change" always has the connotation of change in progress.
You have 240 meters of fence to enclose a rectangular lawn. You are free to make the enclosure have any possible length and width, but you must use all the fence. Play the animation. Move your cursor away from the animation to make the control bar disappear.
| < Previous Section | Home | Next Section > |