| < Previous Section | Home | Next Section > |
In this section we will revisit a topic that we actually first brushed upon in Section 3.13. We will repeat an example from Section 3.13 as an entry to a more advanced idea -- to determine the value of a parameter that maximizes or minimizes the value of a function that models relationships among quantities in a situation.
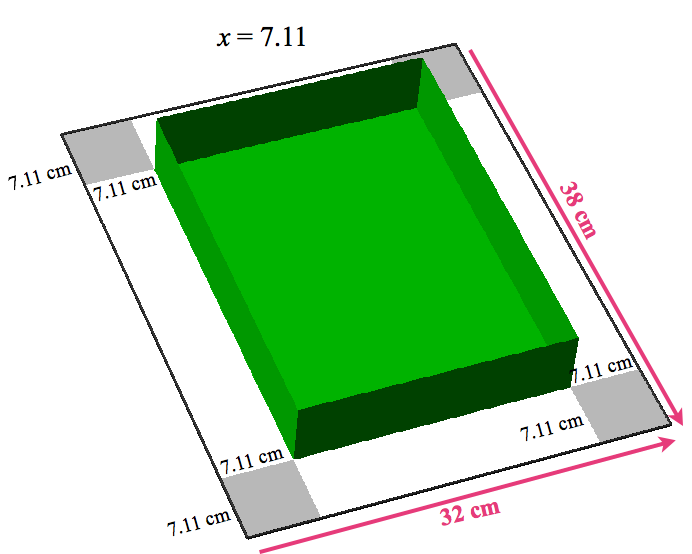
Figure 7.3.1 (originally Figure 3.13.1) shows a 38 cm × 32 cm rectangular sheet of cardboard. You can fold the sheet into a box by cutting a square with side lengths x cm from each of the four corners. The animation in Figure 7.3.1 shows how to fold the sides to make a box.
We finessed a subtle idea in Section 3.13. when discussing this example. It is that we were not thinking of x as a variable in our description of making a box.
We were thinking of x as a parameter. Any value of x determines the size of all four squares, and therefore any value of x determines a unique box. For any particular box, x is a constant. But, different values of x determine differently shaped boxes.
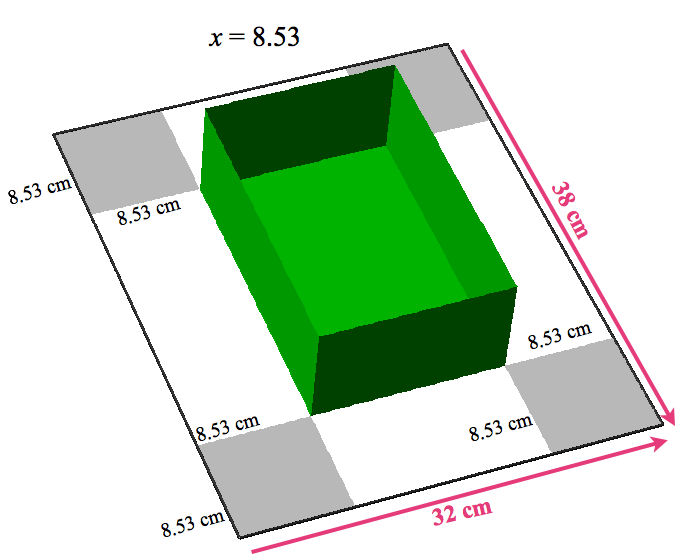
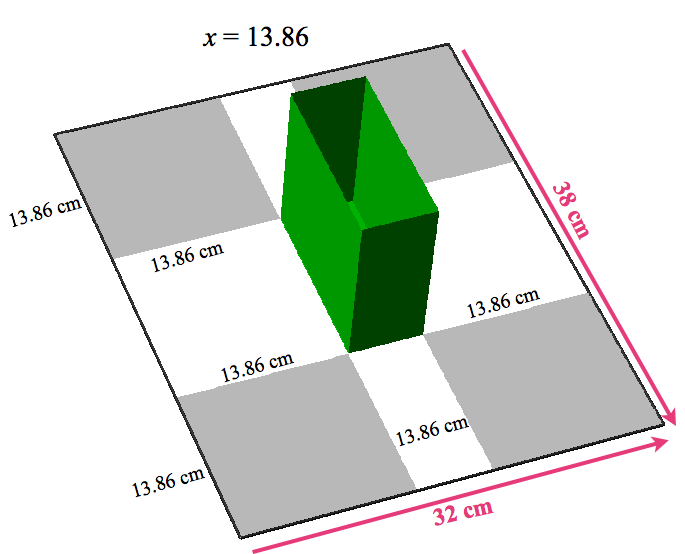
Figure 7.3.2 shows three different boxes that are determined by three different values of x.
 |
 |
 |
Figure 7.3.2. Different values of x determine differently shaped boxes. When x=7.11 we get the left box; when x=8.53 we get the middle box; when x=13.86 we get the right box.
This might seem odd that we used "x" as a parameter. But we did. We thought of x as constant for any one box, but that we could get differently sized boxes by letting x have different values.
It is easy to see that the each box in Figure 7.3.2 has a unique volume for each value of x. Moreover, the box must have a maximum volume because the volume is 0 when $x=0$, it is positive for the three values in Figure 7.3.2, and the volume is 0 when x = 16.
Therefore, the box must have a maximum volume for some value of $x, 0 \le x \le 16$.
It would seem that we should be able to use the tools of calculus to determine the value or values of x that produces a maximum volume. Unfortunately, x is a parameter, not a variable.
However, we can change our meaning for x from being a parameter to x being a variable by varying the way we envision making differently sized boxes.
Instead of envisioning different values of x making a multitude of boxes statically, we can envision one box whose shape we vary just by increasing the width of the square cutout.
Then the square's width will vary from 0 cm to 16 cm, the shape of the box will vary accordingly, and the box's volume will vary as a function of x.
Of course, varying the box's shape by varying the cutout's width is impossible in actuality. But it is possible conceptually.
Figure 7.3.3 illustrates how to think of x as a variable, the cutout's shape as determined by the value of x, and therefore illustrates how to think of the box's volume as varying as the value of x varies.
Figure 7.3.3. Imagine that you make one box by "stretching" the square cutout's width. As you stretch the cutout's width, the box automatically adjusts its dimensions accordingly.Once we have re-conceptualized the situation from envisioning many boxes to envisioning one box whose attributes vary with the value of x, we can use the tools of calculus to determine the value(s) of x that make the box have the largest possible volume:
The volume of a rectangular box is area of base times height.
The area of the box’s base is the box’s width (not the cardboard’s width) times the box’s length (not the cardboard’s length).
We can state each of these relationships as functions of the cutouts’ length conceptually before we worry about defining them computationally.
Then:
| $V(x) = h(x) \cdot A(x)$ | The box’s volume in relation to a
value of x is its height in relation to x times the area of its
base in relation to the value of x. |
| $h(x) = x$ | The box’s height in relation to a value
of x is equal to the length of the cutouts’ sides, which is x. |
| $A(x) = l(x) \cdot w(x)$ | The area of the box’s base in relation to a value of x is the
base’s width in relation to the value of x times its length in
relation to the value of x. |
| $w(x) = 32 - 2x$ | The box’s width in relation to a value of x is 32 cm minus
twice the cutouts’ width. |
| $l(x) = 38 - 2x$ | The box’s length in relation to a value of x is 38 cm minus
twice the value of x. |
We now can define V in terms of a single expression involving x by working from bottom to top in the above list of function definitions:
$$\begin{align} A(x) &= l(x) \cdot w(x)\\[1ex] &=(38-2x)(32-2x)\\[1ex] V(x) &= h(x) \cdot A(x)\\[1ex] &= x\left((38-2x)(32-2x)\right) \\[1ex] &=4x^3-140x^2+1216x \end{align}$$
Now we determine $r_v$ to find critical values of x:
$$\begin{align} r_v(x) &= \frac{d}{dx}\left(4x^3-140x^2+1216x\right)\\[1ex] &= 12x^2-280x+1216\end{align}$$
Solving for x in $r_v(x)=0, 0\le x \le 16$, or for x in $12x^2-280x+1216=0, 0\le x \le 16$, and using the quadratic formula, we find that
$$x=\frac{280 \pm \sqrt {(-280)^2-\left( 4\cdot 12 \cdot 1216 \right)}}{2 \cdot 12},$$or that, to four decimal places, $x=5.7694$ or $x=17.5639$. Since the value of x cannot be larger than 16, the only critical value of x is $x=5.7694$ (to 4 decimal places).
We see that $V''(x)=24x-280$, so $V''(5.7694)=-141.544$. Since $V''(5.7694)$ is negative, $V'(x)$ is decreasing around $x=5.7694$. Since $V'(x)$ is decreasing around $x=5.7694$, $V(5.7694)$ is a maximum. The only other possible extrema are at $x=0$ and $x=16$, and since $V(0)=V(16)=0$, $V(5.7694)=3123.714$ is a global maximum.
We can therefore conclude that as the cutouts' width varies from 0 to 16 cm, the box has its maximum volume of 3123.714 $\text{cm}^3$ when the cutouts' width is 5.7694 cm.
Do not think that the four steps to maximize the box's volume are the most important to remember about this example.
They are important, for sure. However, the most important steps were:
In this important first step, you will use a letter with the meaning of a parameter to represent some quantity's value that is constant in the situation but could change from situation to situation, and then you will re-envision the situation so that this quantity's value varies.
The augmented list of steps in optimizing a situation is:
Step 0 is typically the most difficult and time consuming of all steps. Do not feel uneasy when you find yourself spending a great amount of time in Step 0.
Also, students often skip Step 1. However, if you skip Step 1, then everything is constant and all rate of change functions will have a constant value of 0. While it is true that rate of change functions have a constant value of 0 when all quantities are constant, it is particularly unhelpful when you want to optimize a situation!
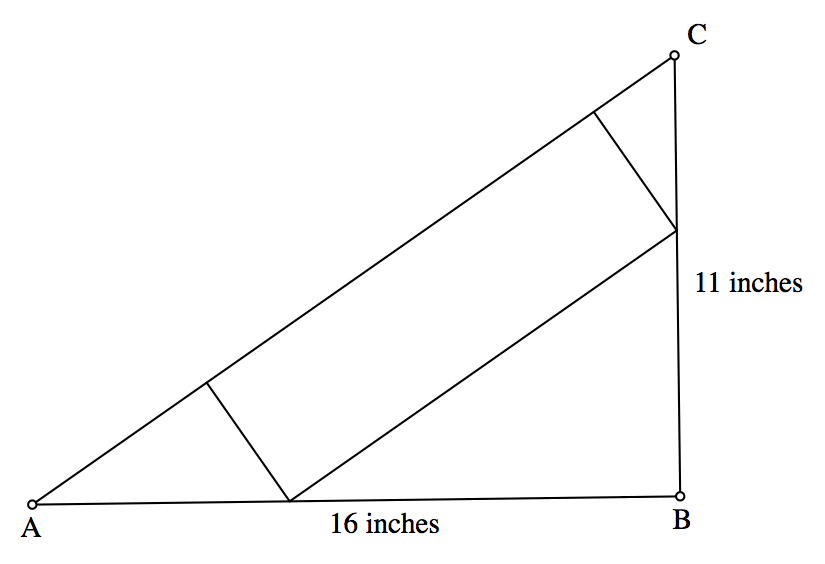
Figure 7.3.4 shows a rectangle within a right triangle constructed so that one side is on the triangle's hypotenuse and the opposite side's endpoints are on the triangle's legs. What dimensions should the rectangle have so that the rectangle has the largest possible area?
Where should one start? With Step 0!! Conceptualize the situation statically, but be alert to quantities whose values are constant in the described situation but will change from situation to situation.
Triangle ABC will not change. But the rectangle's side lengths can vary! Let us label their lengths $S_1$ and $S_2$. We know that the rectangle's area, the quantity we wish to maximize, will be $S_1 \cdot S_2$.
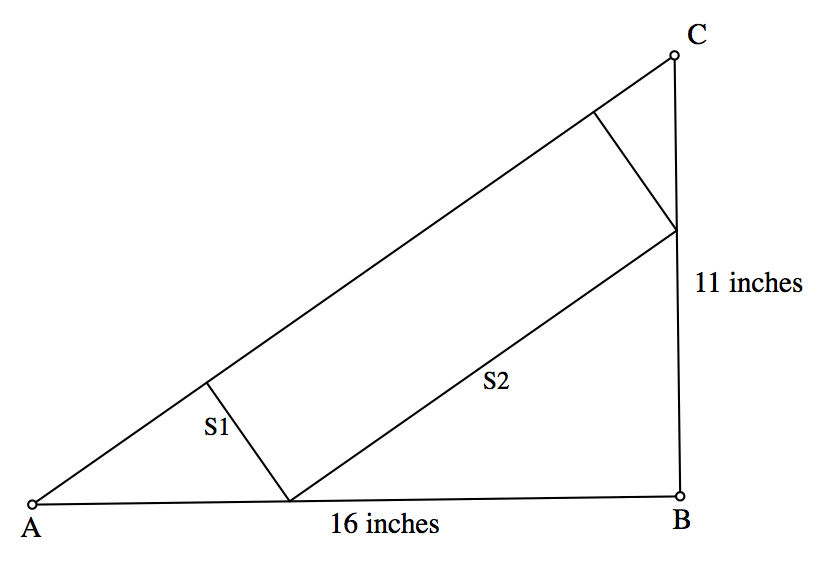
We need to relate $S_1$ to $S_2$. There is no way to do that yet. But there is another quantity that both $S_1$ and $S_2$ depend upon. It is the distance between A and the rectangle's vertex that lies on $\overline{AB}$. Label this value x.
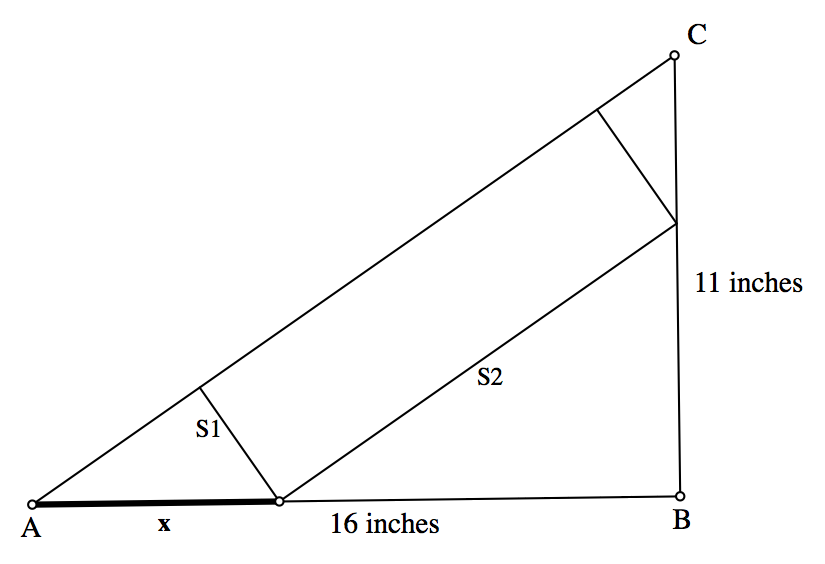
Now we need to relate the values of $S_1$ and $S_2$ to the value of x. Notice -- we are still in Step 0!!
The small triangle having A as one vertex and the segment of length x as its hypotenuse is similar to $\vartriangle \mathrm{ABC}$. Therefore, $$\begin{align}\frac{x}{S_1}&=\frac {\sqrt{11^2+16^2}} {11}\\[1ex]
\text{and hence }S_1 &= \frac{x}{\left(\dfrac{\sqrt{11^2+16^2}}{11}\right)}\end{align}.$$
Likewise, the triangle having B as a vertex and the segment of length $S_2$ as its hypotenuse is similar to $\vartriangle \mathrm{ABC}$.
Therefore, $$\begin{align}\frac{S_2}{16-x}&=\frac {\sqrt{11^2+16^2}} {16}\\[1ex]
\text{and hence }S_2 &= \left(\dfrac{\sqrt{11^2+16^2}}{16}\right)(16-x) \end{align}.$$
If we let A represent the rectangle's area, then $A=S_1 \cdot S_2$. Remember, we are still in Step 0!!
Expressing A in terms of x we have: $$\begin{align}
A &=S_1 \cdot S_2\\[1ex]
&=\left(\frac{x}{\left(\dfrac{\sqrt{11^2+16^2}}{11}\right)}\right)\left(\dfrac{\sqrt{11^2+16^2}}{16}\right)(16-x)\\[1ex]
&=\frac{11}{16}x(16-x)\end{align}$$
Step 1: Re-conceptualize the situation dynamically, so that the key parameter (x) becomes a variable.
As the value of x varies, the rectangles sides will vary (to remain a rectangle) and therefore the values of $S_1$ and $S_2$ will vary as the value of x varies.
Step 2: Define a function that relates the key variable to the value of the quantity you want to maximize or minimize.
$$A(x)=\frac{11}{16}x(16-x)$$
Step 3: Determine the rate of change function, $r_A$. $$\begin{align}r_A(x)&=\frac{d}{dx} \frac{11}{16}x(16-x)\\[1ex]&=\frac{11}{16}\frac{d}{dx}\left(16x-x^2\right)\\[1ex] &=\frac{11}{16}(16-2x)\end{align}$$
Step 4: Determine critical values
The only critical value of x is when $r_A(x)=0$, or when $x=8$.
Step 5: Test critical values and interval endpoints (if any) for local and global maxima or minima
$A''(x)=\frac{11}{16}(-2)\text{, so }A''(8)$ is negative, and therefore $r_A(x)$ is decreasing around $x=8$. This tells us that $A(8)=44$ is a maximum.
Since $A(0)=A(16)=0, A(8)=44$ is a global maximum, and therefore the largest possible rectangle has an area of 44 $\text{in}^2$. This happens when $x=8$. According to the formulas that relate $S_1$ and $S_2$ to x, $$S_1 = \frac{8}{\left(\dfrac{\sqrt{11^2+16^2}}{11}\right)}$$and $$S_2 = \left(\dfrac{\sqrt{11^2+16^2}}{16}\right)(16-8),$$or $S_1= 4.532$ and $S_2=9.708$ (to 3 decimal places).
Suppose that the triangle in Example 2 has a length of L (instead of 16) and a height of H (instead of 11). Determine the value of x that maximizes the rectangle's area. (Your answer will be in terms of L and H.)
Follow Steps 0 to 5, as illustrated in
this section, for each of the remaining exercises. Be sure to draw
diagrams as part of Step 0.
Of all rectangles with a perimeter of 100 cm, which one has the largest area?
A rancher has 400 meters of fencing. He will fence a rectangular corral next to a cliff. He will use all 400 meters to make just 3 sides of the rectangle. He wants to make a corral that will hold as many cattle as possible, so he wants the corral to contain the largest possible area. How long and how wide should he make the corral?
Which two positive real numbers with a product of C have the smallest possible sum?
Which two positive real numbers with a sum of D have the largest possible product?
See the animation below.
Determine the coordinates of the point(s) on the graph of $y=(x-2)^3+2(x-2)^2-1$ on the interval $[0,3.12]$ that are farthest from the point with coordinates $(1.5,1)$.
Create a story problem about a concrete situation that parallels the structure of Question 9. Interpret its solution.
An A-frame barn is to be built so that it is 30 ft high, 40 ft wide and 60 ft long. A rectangular room is to be built inside the barn so that the room's ceiling abuts the roof. What dimensions should the room have so that its volume is as large as possible?
A 5324 cubic foot tank with a square base and an open top is to be constructed from a sheet of steel so that the tank's height is half its width. Each side of the tank will be cut from the steel plate and the sides will be welded together. The manufacturer observed that many tanks of different dimensions could be made to hold 5324 cubic feet. What dimensions should the tank have so that it uses the least amount of steel?
| < Previous Section | Home | Next Section > |