Section 5.1
Introduction to Accumulation Functions

Basketball Rocket	Approximate Rate of Change Functions	Define Approximate Rate of Change Function
Concept of Differential Redux	Define Left(t) Conceptually	Define Approx Accum Function Conceptually
Exercise Set 5.1

In Chapter 4, Section 4.9 we developed the idea that knowing a function’s rate of change at a moment of its independent variable gives information about how much the function varies during that moment:

If a function f has an exact rate of change of $r_f(x_0)$ at the moment $x=x_0$, then the variation in f during that moment is essentially equal to $r_f(x_0)dx$ as $dx$ varies through that moment.

We do not know f's value at any moment, but we have a good approximation of how much it varies during any moment. We will return to this idea repeatedly.

The concept of an accumulation function is quite general.

When the measure of Quantity A varies at some rate of change with respect to the measure of Quantity B, Quantity A accumulates variations at a rate that is essentially constant in relation to sufficiently small variations in B. From Chapter 4, this is the meaning of Quantity A having a rate of change at a moment of Quantity B.

Defining a function whose values give the net accumulation of one quantity by knowing its rate of change at every moment of its accumulation addresses the first foundational problem of calculus. Namely,

First Foundational Problem of Calculus

You know how fast a quantity varies at every moment; you want to know how much of that quantity there is at every moment.

When we know a function’s rate of change at every moment of its independent variable, we can estimate the function’s net variation as its independent variable varies. We do this by accumulating variations in the function’s value as they occur while the value of its independent variable passes through successive moments.

An accumulation function is a function that is generated by accumulating variations in its value. The variations occur at some rate over moments of its independent variable.

In the remainder of this chapter we will

Develop the idea of approximating net variation in an unknown accumulation function when all we know is how fast it varies at every moment.
Develop a method for representing these approximations so GC can compute them for us.
Introduce a representation of exact accumulation functions from exact rate of change functions that GC will understand.

Reminder to Windows users: You cannot type "$\Delta x$", "$\Delta t$" etc. in GC. Instead, type "\Dx\", "\Dt\", etc. Windows gives no easy way to type the character "∆".

Reminder to Mac users: To type "$\Delta x$", "$\Delta t$" etc. in GC, type "\option-j x\", "\option-j t\", etc. The keystroke option-j gives the character "$\Delta$" on a Mac.

Example: A Basketball rocket

A team of enginering students designed a rocket-powered basketball for their course project.

They designed the motor so that within the first 90 seconds after launch, the rocket will have a rate of change of height with respect to time (i.e., velocity) of $t^{1.3}$ m/s t seconds after the motor starts. That is, they know that the rocket’s rate of change function $r_h$ will be $r_h(t)=t^{1.3},\, 0\le t \le 90$.

Figure 5.1.1 shows how the team anticipates the rocket’s velocity will vary with time.

Figure 5.1.1. The basketball rocket. Engineers have designed the rocket so that at t seconds after the motor starts, its velocity will be $r_h(t)=t^{1.3}\text{, }0\le t \le 90$.

The team must also predict the rocket’s altitude at each moment because they have maneuvers to program that are based on the rocket’s altitude.

Unfortunately for them, their rocket will have a clock, but not an altimeter. Their problem, then, is to develop a function h such that $h(t)$ will give the rocket’s height at each moment after the rocket is launched when all they can predict is the rocket’s velocity at each moment.

The solution to defining h would be simple if the rocket rose at a constant velocity k. The rocket’s altitude would be $h(t)=kt$. Unfortunately, the rocket’s velocity is not constant over any interval of time within 90 seconds after launch. On the other hand, its velocity is essentially constant over sufficiently small intervals of time within 90 seconds after launch.

The team cannot determine a definition of $h$. However, they can approximate values of $h(t)$ by drawing on their understanding of rate of change at a moment:

The function $r_h(t)=t^{1.3}$ gives the rocket’s exact rate of change of altitude with respect to time at each moment in time since launch.
This means, for example, that at $t=2.1$ seconds after launch, the rocket will rise at a rate of change that is essentially $r_h(2.1)=2.1^{1.3} \mathrm{m/s}$ for a brief interval of time that contains $t=2.1$.
As the value of t varies through this interval, or as $dt$ varies from 0 to the width of the interval, $dh$, the approximate variation in h as t varies, will be essentially $dh=r_h(2.1)dt$.
The team can approximate any value $h(t_0)$ for $t=t_0$ by adding all the variations in $h$ as t varies from 0 to $t_0$ through intervals of time small enough that $r_h(t)$ is essentially constant through each.

The team’s dilemma at this juncture is that they do not know the widths of the time intervals over which $r_h(t)$ is essentially constant. Were they to know these widths, they could get the accumulated variation in altitude from $t=0$ to any current value of t by adding all the variations in h that accumulate over these intervals of time.

However, they can experiment with values of $\Delta t$ and use an approximate rate of change that is constant over these intervals.

Suppose the function h has essentially a constant rate of change throughout time intervals of length $\Delta t=0.1$ seconds. We will use $A$ to name the function whose values $A(t)$ approximate values of $h(t)$. Reminder: Values of h(t), the unknown height function, give the rocket's exact height t seconds after launch. A(t) will approximate h(t) for values of t.

Throughout the first two seconds, the rocket would rise $$A(2)=r_h(0)(0.1)+r_h(0.1)(0.1)+r_h(0.2)(0.1)+...+r_h(1.9)(0.1)$$

A is the accumulation function that approximates the exact accumulation function h. We can write $A(2)$ concisely by using summation notation:
$$\color{red}{\text{(Eq. 5.1.1)}}\qquad A(2)=\sum_{k=0}^{19}r_h(k\Delta t)\Delta t$$

In principle, the team's approach to solving its problem starts by cutting up the time axis into intervals of width $\Delta t$ (generically, "$\Delta t$-intervals").

They will then assume that h has rates of change that are essentially constant over each $\Delta t$-interval.

What value of $r_h$ should they choose as the constant value $r_h(t)$ as t varies through an interval?

Actually, there is no "should" in their choice. A better question is what would be a convenient choice for the value of t at which to evaluate $r_h(t)$ as the essentially-constant rate of change of h over the interval. They chose, for convenience, the value of $r_h$ at the beginning of each $\Delta t$-interval.

Figure 5.1.2 uses the ridiculously large value of 0.9 seconds as the width of each $\Delta t$-interval. This is just to make it easy for you to visualize how this approach works.

Figure 5.1.2. Values of the function r approximate values of the exact rate of change function v. Values of the function A approximate values of the exact accumulated altitude as t varies within the first 8 intervals.
Move your pointer away from the animation to hide its control bar.

You must examine Figure 5.1.2 in a particular way to understand all that is going on in it.

First, partition the time axis in both graphs into intervals of length 0.9 starting at 0. It is over these intervals we pretend that the rocket’s altitude varies at essentially constant rates of change.
The constant rates we assume are the velocities at the beginning of each interval. ($r_h(t)=0$ at the beginning of the first $\Delta t$-interval.)
As the value of t varies, the value $r_h(t)$ at the beginning of each interval in the left graph is the constant velocity we pretend for the rocket over that interva.
GC’s graph on the right side of Figure 5.1.2 is a simulation of how the rocket’s accumulated altitude varies given the velocity is constant over each $\Delta t$-interval.
The graph on the right of Figure 5.1.2 is of the function $A$, the approximate altitude function whose values are determined by out assumption of constant velocities over $\Delta t$-intervals.
Even though the two graphs in Figure 5.1.2 look similar, it is only because the vertical axis in the right graph is compressed vertically to fit in the diagram.

In Figure 5.1.2 we assume that the rocket’s altitude varies at a constant rate throughout each $\Delta t$-interval, starting at $t=0$. We also assume that the constant rate over an interval of t is the value of $r_h$ at the beginning of the interval.

GC’s graph on the right side of Figure 5.1.2 shows the accumulated variations that happened by assuming that h varies at a constant rate over each of its $\Delta t$-intervals.

Our goal is to create a system of function definitions that we can "hand" to GC so it does all our computations for us.

To accomplish this goal we must first conceptualize the functions we want to eventually define. That is, we must conceptualize

A function that has a constant rate of change over every sub-interval of our domain, and this function approximates the exact rate of change function
A function that computes approimate accumlation from the approximate rate of change function described above.

Defining a function conceptually is to focus on what you want the function to do without bothering about how to make the function do it. With these functions conceptualized, we will create definitions from them that GC can compute.

Conceptualizing Approximate Rate of Change Functions

Figure 5.1.2 is repeated below. Play it again. At the end, you see what might look like "sticks" jutting from the graph of $y=r_h(t)$ where $r_h(t)=t^{1.3}$.

It is important to understand these "sticks" are actually the graph of a function. The function having these "sticks" as its graph is the function r where every value $r(t)$ is the rocket's velocity at the left end (beginning) of the $\Delta t$-interval containing that value of t.

Figure 5.1.2a (below) illustrates the general idea of defining a new function from values of a given function so that the two are equal at the beginning of a $\Delta x$-interval, but one of them retains that value throughout the $\Delta x$-interval.

Every value $r(x)$ is the value of $r_f$ at the beginning of the $\Delta x$-interval containing that value of x. The function left(x), which we will define computationally later in this chapter, represents the left end of the interval containing the current value of x. Notice: The value of left(x) is on the x-axis. It is the value of the hash mark at the beginning of the current $\Delta x$-interval.

Figure 5.1.2a Understanding the graph of $r(x)$ in relation to the graph of $r_f(x)$. Every value $r(x)$ is the value of $r_f$ at the beginning of the $\Delta x$-interval containing that value of x.

Define an Approximate Rate Function

Our assumption that h varies at a constant rate over each $\Delta t$-interval forces us to assume an approximate rate function r (left graph in Figure 5.1.2) which is constant over each $\Delta t$-interval. All these assumptions produce a function A (for "approximate accumulation"). Values of A comprise an approximate altitude function that is composed of approximate variations in altitude.

Let r be the approximate rate function illustrated in Figure 5.1.2. This is the function that has a constant value as t varies through each $\Delta t$-interval, where $\Delta t=0.9$ and $k\in \{1,2,\cdots\}$. We can therefore define the approximate rate of change function r piecewise as in Equation 5.1.2.

$$\color{red}{\text{(Eq. 5.1.2)}}\qquad r(t)=\begin{cases} r_h(0\cdot 0.9) &\text{if $0\cdot 0.9\le t \lt 1\cdot 0.9$}\\[1ex] r_h(1\cdot 0.9) &\text{if $1\cdot 0.9\le t \lt 2\cdot 0.9$}\\[1ex] r_h(2\cdot 0.9) &\text{if $2\cdot 0.9 \le t \lt 3\cdot 0.9$}\\[1ex] &\vdots\\[1ex] r_h((k-1)\cdot 0.9)&\text{if $(k-1)\cdot 0.9 \le t \lt k\cdot 0.9$}\\[1ex] &\vdots \end{cases}$$

Reflection 5.1.1. Let r be defined as in Equation 5.1.2. Complete this table. Recall $r_h(t)=t^{1.3}$.

t	*r(t)*
0.5
0.6
1.2
1.3
1.4
2.71
2.72
2.95

It is worthwhile to note there are two types of variation happening in Figure 5.1.2:

variation within a current $\Delta t$-interval (the $\Delta t$-interval containing the current value of t)
variation of the completed $\Delta t$-intervals (the $\Delta t$-intervals through which the value of t has passed). Figure 5.1.3 illustrates the distinction between completed and current $\Delta t$-intervals.

Figure 5.1.3. Distinction between current and completed $\Delta t$-intervals.
Move your pointer away from the animation to hide its control bar.

Using values of r to compute approximate variations in the exact accumulated altitude function h, we get the function A, the accumulation function that approximates the exact accumulated variations in altitude:

$$\color{red}{\text{(Eq. 5.1.3)}}\qquad A(t)= \begin{cases} r(t)(t-0) &\text{if $0\le t \lt 0.9$}\\[1ex] \left(r(0)\Delta t\right)+r(t)(t-0.9) &\text{if $0.9\le t \lt 1.8$}\\[1ex] \left(r(0)\Delta t+r(0.9)\Delta t\right)+r(t)(t-1.8) &\text{if $1.8\le t \lt 2.6$}\\[1ex] \left(r(0)\Delta t+r(0.9)\Delta t+r(1.8)\Delta t\right)+r(t)(t-2.7) &\text{if $2.7\le t \lt 3.6$}\\[1ex]\text{... and so on}\end{cases}$$

There are two things to notice about Equation 5.1.3.

The general pattern of Equation 5.1.3 is that approximations of accumulated altitude for any value of t are calculated in two parts: what we might call "completed variation" and "current variation".

"Completed variation" is the variation in altitude that happened in the complete $\Delta t$-intervals the value of t passed through prior to the $\Delta t$-interval it is currently in.

This completed variation is represented by an expression like $\left( r(0)\Delta t+r(0.9)\Delta t\right)$. This expression represents the rocket's approximate variation in altitude according to the hypothetical scenario that it passed through the interval $[0, 0.9]$ seconds at $r(0)$ meters/sec and through the interval $[0.9, 1.8]$ seconds at $r(0.9)$ meters/sec.
"Current variation" is the approximate variation in altitude that has happened from the beginning of the current $\Delta t$-interval (the one that contains the current value of t) to the current value of t as t varies.

This is just $dy = m \cdot dt$, where dy is the variation in altitude as dt varies through the interval from 0 to $\Delta t$ seconds, and m is the rocket's velocity at the beginning of the current $\Delta t$-interval.
Keep in mind that the current value of t varies as time passes, so both "completed variation" and "current variation" vary as time passes. "Completed variation" varies in chunks while "current variation" varies continuously.

The variation in approximate accumulated altitude happens within the current $\Delta t$-interval and is computed by multiplying the constant velocity we pretend the rocket travels within the current $\Delta t$-interval and the amount of time it has traveled within the current $\Delta t$-interval.

The amount of time that the rocket has traveled within the current $\Delta t$-interval is $t-\mathrm{left}(t)$.
The constant rate at which the rocket travels is $r(t)=r_h(\mathrm{left}(t))$, the ball's velocity at the left end of the current $\Delta t$-interval.

The Concept of Differential, Said Another Way

We use the letter "d" preceding a variable to mean that the variable's value "varies a little bit".

The way to envision a differential is to first keep in mind that a variable represents the value of a quantity whose value varies. Variables vary, always.

Another key idea in understanding differentials is that they are variables whose values vary "a little bit". To vary a little bit, they must vary from somewhere. We therefore think of differentials of an independent variable as varying through fixed intervals in the variable's domain.

Finally, a differential is a variable by which another variable varies. This surely sounds confusing. The figure below illustrates this idea. The term "left(x)" in the animation means the left end of the interval containing the current value of x.

Variables and Differentials. The value of x varies smoothly through its domain. Differentials in x (dx) are small variations in the variable's value. The symbols "dx" and "$\Delta x$" have different meanings.

Define a function conceptually that gives the left end of an interval

As the value of t varies, it is always within some $\Delta t$-interval. We will use "left(t)" to represent the number at the beginnning of the $\Delta t$-interval containing the current value of t.

left(t) = the value of the left end of the $\Delta t$-interval containing the current value of t.

Figure 5.1.4 illustrates the concept of left(t). It shows the independent axis partitioned into $\Delta t$-intervals of size 0.9.

Figure 5.1.4. The meaning of the function left(t) and its relationship with t, $\Delta t$, and dt. In this figure,
a=0 and $\Delta t=0.9$. The value of left(t) is the value of the left end of the $\Delta t$-interval containing the current value of t.

As t varies from 0, its current value of t is always within some $\Delta t$-interval. The value of left(t) is the value of the left end of the $\Delta t$-interval containing the current value of t. The value of $dt$ is the difference between the value of t and the value of left(t). Therefore $dt=t-\mathrm{left}(t)$ as the value of t varies in the interval $\mathrm{left}(t)\lt t \le \mathrm{left}(t)+\Delta t$.

Another way to think of left(t) is given in Figure 5.1.4a. It shows that with a = 0 and $\Delta t$ = 0.9, every real number within a ∆ t-interval is mapped to the number that begins that interval. Figure 5.1.4b shows the same thing except that it leaves a record of how values of t are mapped to values of left(t).

Figure 5.1.4a. The top number line shows values of t varying continuously from 0 to 3.5. The bottom number line shows values of left(t) as t varies continuously.
Move your pointer away from the animation to hide its control bar.

Figure 5.1.4b. The top number line shows values of t varying continuously from 0 to 3.5. The bottom number line shows values of left(t) as t varies continuously. The video shows the record of the mapping $t \to \mathrm{left}(t)$.
Move your pointer away from the animation to hide its control bar.

We can now summarize Equation 5.1.2 in one line: $$\color{red}{\text{(Eq. 5.1.4)}}\qquad r(t)=r_h(\mathrm{left}(t))$$

Define Approximate Accumulation Function Conceptually

Now that we have left(x) defined conceptually, we can summarize the conceptual definition given in Equation 5.1.3 in one line:

Equation 5.1.5. The approximate accumulation function in one line.

Using $\Delta t=0.9$ clearly does not give good approximations for values of h, the exact accumulated-altitude function that we seek to approximate. We can get better approximations by making the value of $\Delta t$ smaller.

Figure 5.1.5 shows the same method as shown in Figure 5.1.2, but with $ \Delta t=0.5$. GC’s graph on the right is a simulation of the rocket’s accumulated altitude given that it varied according to the approximate altitude function A with $a=0$, $\Delta t=0.5$, $r_h(t)=t^{1.3}$, and $r(t)=r_h(\mathrm{left}(t))$.

Figure 5.1.5: Partition the time axis into intervals of length 0.5 starting at $a=0$; we pretend that the rocket’s altitude varies at essentially constant rates of change during these intervals. The constant rates we assume are the values of v at the left end of each interval.
Move your pointer away from the animation to hide its control bar.

You must understand all that is going on in Figure 5.1.5 in order to represent what is going on symbolically.

Partition the time axis in the left side of Figure 5.1.5 into $\Delta t$-intervals of size 0.5 seconds.
This imposes a partition of the time axis for the accumulation function on the right side into $\Delta t$-intervals of size 0.5 seconds.
As the value of t varies from $a=0$, the function r defined as $r(t)=r_h(\mathrm{left}(t))$ is constant over each $\Delta t$-interval (see left side of Figure 5.1.5).
The function A (on the right of Figure 5.1.5) varies with respect to t at the constant rate of $r(t)$ within each $\Delta t$-interval, and is therefore linear over each $\Delta t$-interval (whether completed or current). The variation in A as t varies within a current $\Delta t$-interval is represented by the expression $r(t)(t-\mathrm{left}(t))$.
The variation in A over completed $\Delta t$-intervals prior to the current $\Delta t$-interval is made by the value of t having passed through each of them. The completed accumulation is represented by the expression

The accumulation from the value of a to the current value of t is the sum of the bits of accumulation over completed ∆ t-intervals plus the accumulation during the current $\Delta t$-interval. Equation 5.1.5, repeated below, expresses this idea symbolically.

where t is the number of seconds elapsed since launch, $r(t)$ is the ball's velocity at the beginning of the $\Delta t$-interval containing the value of t, and A(t) approximates the rocket's altitude at that number of seconds.

Reflection 5.1.2. The definition of A given above defines the upper limit of the sum conceptually. It does not use a formula for actually calculating an upper limit. Does this matter in terms of defining the function A? Explain.

Reflection 5.1.3. The definition of A uses the function named "left" even though left(x) is still not defined computationally. Does this matter in terms of understanding how the definition of A is supposed to work? Explain.

Reflection 5.1.4. Why is it important to use "number of complete ∆t-intervals from a to t" as the upper limit of the summation?

Reflection 5.1.5. How does the term $r(t)(t-\mathrm{left}(t))$ in Equation 5.1.5 represent "accumulation so far in the current $\Delta t$-interval"?

Exercise Set 5.1

For Questions 1 - 3. Consider the video below. It shows a ball hanging from a board by a rubber cord. The ball hangs at rest 10 feet below the board. At $x = 0$ seconds, the ball is set in motion with a quick shove downward, causing the rubber cord to stretch and the ball to bounce. The graph shows the rate of change of the ball's displacement from rest with respect to elapsed time, which is the velocity function $v(x) = -\mathrm{cos}(x)$.

Here is a printable version of the ball's velocity graph. Sketch an approximate velocity function for the bouncing ball scenario on the graph, and fill in the 2nd column 'Approx Velocity' in the table below (click here for a printable version). (You'll do the 3rd and 4th columns later). Determine the approximating constant velocities using intervals of length 0.5 seconds, with each constant velocity equal to the true velocity at the left end of the interval.
Fill in columns 3 and 4 of the table you printed from Exercise 5.1.1 based on your approximate velocities and the mathematics of constant rate of change. Are these values exact or approximate?
The graph below shows the function that gives the approximate net accumulated variations in the ball’s displacement from its resting position relative to elapsed time. It is linear over each $\Delta x$-interval. The graph shows the ball's approximate displacement y, in feet, from its resting position, x seconds after the ball was put in motion.

Why is the graph linear over $\Delta x$-intervals?
How are individual values from the first few rows of the table reflected in the portion of the graph shown above? Label each element of the given portion of the graph with the appropriate variable and table value. (Hint: columns 3 & 4 both apply!)
Complete the graph in the manner as the portion presented below, including all elements, and labeling each element of your sketch with variables and values from the table.
Use the graph you made in part (c) to sketch a second graph showing the ball's distance traveled at each moment after the ball was pushed.

A bacterial culture began with 10,000 bacteria. The graph below (click here for a printable version) shows the rate, measured in bacteria per hour, at which the number of bacteria grew at each moment in time (measured in hours) after the culture was first observed. The rate fluctuated because the culture’s environment fluctuated.

Use the method illustrated in this section to build an approximate accumulation function B, whose values are the number of bacteria in this culture t hours after the initial observation.

Sketch an approximate rate of change function on the above graph for $t = 0$ to 3.2 hours and $\Delta t=0.4$ hours. Each constant rate of change will be the actual rate of change at the left end of its respective interval.
Using your sketch of the modified rate function and estimates of rates of change from the displayed graph, calculate the variation in bacteria population in the first 1.6 hours. Show all your work. The constant rates you use will be estimates from the graph, since no function rule for the rate of change is given.
Repeat question b. to estimate the variation in bacteria population in the first 2.1 hours.
Besides using a different number of intervals and getting a different answer, what was different about computing the answer for part c. compared to part b?

Explain the phrases "completed intervals" and "current interval"? After explaining these phrases, relate them to the calculation you made in part c.
Based on your estimates in parts b. and c, estimate the population of bacteria at 1.6 and 2.1 hours.
Estimate the variation in bacteria population from t = 2 to 3 hours. Show your work.

In a test drive of a new fuel efficient car, a company tracks the car's mpg (miles per gallon) for 2 gallons of gasoline burned during a test drive. Use the approximating method developed in this section with intervals of 0.25 gallons of gasoline and the "left end" approach to complete the items below. (Click here for a printable version.)

Based on the specifications given in the instructions above, sketch the pretend mpg rate function on the same axes as the given mpg curve.
Represent numerically approximations for the variations in the number of miles driven and the cumulative number of miles driven for every 0.25 gallons of gasoline burned.
Represent the cumulative number of miles driven graphically, also showing the variations in distance for every 0.25 gallons on your graph.
Approximate the variation in miles driven for the first 0.9 gallons burned. Explain your calculations in terms of "completed intervals" and "the current interval."

In each of (a) through (e), determine the number of completed ∆x-intervals between the given value of a and the given value of x. Have the aim of stating a general method for finding the number of ∆x-intervals between any value of a and any value of x.

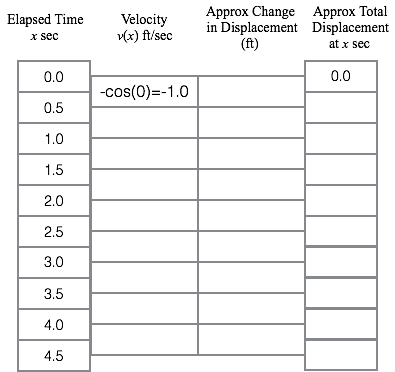
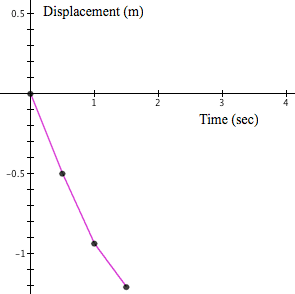
	Value of a	Value of x	∆x	No. of complete ∆x-intervals between a and x
a)	2	17	0.03
b)	3.2	5.23	0.0125
c)	-3	-1.2	0.025
d)	-1	-5	1.2
e)	5	128.3	0.2

Enter a sum into GC that will compute A(4.72) given that $a=2$, $\Delta t=0.01$ and $r_f(x)=\sin(x)$. Type ctrl-shift-S to get a summation sign.
Download and print this file. Draw arrows between the symbolic statements and the part(s) of the figure that they represent.
Let $r_g$ be defined as $r_g(t)=e^{-.5t}$ and let $a=0$. Have GC calculate A(1.72) using:

a) $\Delta t=1$

b) $\Delta t=0.1$

c) $\Delta t=0.01$

d) $\Delta t=0.001$

e) $\Delta t=0.0001$

f) Now describe the trend in the values of A(1.72) with respect to values of $\Delta t$ in parts (a) - (e).

Suppose that $\Delta x=0.125$, $a=2$, and $r_f(x)=x\cos(x)$. What will be the numerical value of the 134th term in $\sum_{k=1}^{500} r(a+(k-1)\Delta x) \Delta x$ ?
The Basketball Rocket engineering team was meeting one afternoon. Rachel ran into the meeting room, exclaiming

We made a mistake on the velocity function! It is actually $$r_h(t) = 15 \frac{2^{t-10}}{2^{t-10}+1}.$$

a) What needs to be changed in the system of statements that describe how to calculate approximations of the rocket’s height for values of elapsed time?

b) What would the graph of elevation relative to elapsed time look like now?

Each of (a) through (d) is GC’s displayed graph of an exact rate of change function for an accumulation function. Let $a=-1$ and $\Delta x=0.001$ for each of (a)-(d). For each graph, sketch a graph of $y=A(x)$ that you anticipate that GC would produce. Click the solution link on each line after you have sketched your anticipated graph of $y=A(x), x≥a$.

Solution

A function f has $r_f(x)=x(x-1.3)$ as its exact rate of change function. Here is a table of values of x, values of $r_f(x)$, approximate variations in f, and approximate net accumulation as a function of x, all with $\Delta x=0.02$ and $a=1$.